Density Estimation and Combination under Model Ambiguity

¹ Σ ln f^cn(^χl
n _i g(xi)

Let define

f_n (xi) - g(xi)

g(xi)

, ¹ X ∕^fn(^xi) ^-^g(xi)∖ 3 3

⁺ 2n ¾ g(χi) J ≤ u.

(56)

Vb₁_n

n ∑(

c(xi) ^- g(xi)
g(xi)

and

2
_b 1 fn (xi) - g(xi)

^v2ⁿ = n M --^l x ) ) ■

By Lemma 3.1 Hong-White (2000), under assumption A1 and A2, nh⁴/ ln n →∞,h→ 0. Then:

KcI1 = V^b1n

- V2n+ + Op(n ²h ³lnn + h⁶).

(57)

AT 1 1 1 JlJ T^T∙ 1 T^T∙ T J 1 1 it X 1 1 —1 T xt—x — —X ZXl 1

Now we have to analyze the terms Vin and V2n. Let define f(x) = ʃh ¹K( ⁱ- )g(x)dx and

h^—iKh(xi
an(xi,xj ) = ----------

^-^xj ) ^- f^h

ⁱKh (xi - x)g(x)dx

g(xi)

bn(xi) = —

iKh∣^χΛ-^χ)f(^χ)dx-g(^χi)
g(xi)

Then

V^b1n

c(χi) - f (χi) + f (χi) - g(xi)
g(χi) g(χi)

n(n — ι)h Σ Σ aⁿ(xⁱ^{, x}^j) ⁺ n Σ bⁿ(xⁱ) =
i j,i6=j i

(58)

= V11n +B

where Viin is a second order U-statistic and it will affect the asymptotic distribution of KIi. Similarly to

TT ιι<₁nnn TJ ∙. Γ' ■ . ι 1- n ■

Hall(1984) let rewrite Vii_n in the following way:

Viin = -_rn(n

₁y∑ ∑Hin(Xi,Xj)

i j,i6=j

1 Kh (xj

Hin(xi, ^χj) = 2h (

Xi) - KΚh(x - Xi)g(x)dx + K_h(xi
g(xi)

xj) - Kh(xi - x)g(x)dx

= J ] — Jn(^xi^,xj) + Jn(^xj ^,xi)

g(xi)

(59)

E(H1_n (xi,xj)/xi)=0, then using Theorem 1 in Hall(1984) we can show that

^ I

Viin = < -_rn(n

_π∑ ∑Hiin(Xi,Xj)
i j,i6=j

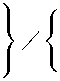
2E [H2n(^χi^,xj

n²

-)ɪ I →^d N(0,1).

(60)

E [J‰1XJ)] ,_h / Kh

xi) ^- RKh(xi ^-^χ)g⁽^χ)^dχ¢²

------g₂∣_x )------------------g(xi)g(xj)dxidxj =

CorPapers

Density Estimation and Combination under Model Ambiguity

More intriguing information