1.3 Definitions and basic characteristics
Dependence on alpha
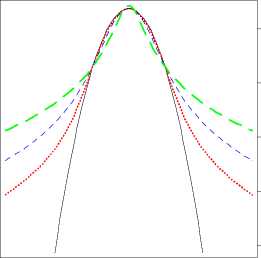
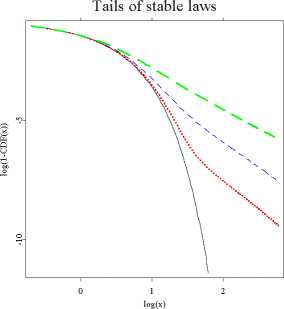
Figure 1.1: Left panel : A semilog plot of symmetric (β = μ = 0) α-stable
probability density functions (pdfs) for α = 2 (black solid line), 1.8
(red dotted line), 1.5 (blue dashed line) and 1 (green long-dashed
line). The Gaussian (α = 2) density forms a parabola and is the
only α-stable density with exponential tails. Right panel: Right
tails of symmetric α-stable cumulative distribution functions (cdfs)
for α = 2 (black solid line), 1.95 (red dotted line), 1.8 (blue dashed
line) and 1.5 (green long-dashed line) on a double logarithmic paper.
For α < 2 the tails form straight lines with slope -α.
ɑ STFstab01.xpl
exhibit a power-law behavior. More precisely, using a central limit theorem
type argument it can be shown that (Janicki and Weron, 1994; Samorodnitsky
and Taqqu, 1994):
limx→∞ xαP(X > x) = Cα(1 + β)σα,
(1.1)
limx→∞ xαP(X < -x) = Cα(1 + β)σα,
where:
Cα
=20
sin(x)dx
= 1Γ(α) sin πα.
π2
The convergence to a power-law tail varies for different α’s and, as can be seen
in the right panel of Figure 1.1, is slower for larger values of the tail index.
More intriguing information
1. The name is absent2. The name is absent
3. The name is absent
4. The name is absent
5. Qualifying Recital: Lisa Carol Hardaway, flute
6. What should educational research do, and how should it do it? A response to “Will a clinical approach make educational research more relevant to practice” by Jacquelien Bulterman-Bos
7. Asymmetric transfer of the dynamic motion aftereffect between first- and second-order cues and among different second-order cues
8. Evolving robust and specialized car racing skills
9. The resources and strategies that 10-11 year old boys use to construct masculinities in the school setting
10. Globalization, Redistribution, and the Composition of Public Education Expenditures