Second Order Filter Distribution Approximations for Financial Time Series with Extreme Outlier

J.Q. Smith and Antonio Santos

ple, in the second sub-sample we compared the density f (α₈₅₂∖y 1,... ,y₈₅₂,θ) with
f (α₈₅₂∖y 1,... ,y1000,θ), which we might have expected to be close. The difference
between the filter distribution obtained using the first order particle filter was enor-
mous in comparison with the smoothing distribution. The same did not occur with
the second order particle filter, which is a clear indication of the feasibility of the
procedures presented in this paper.

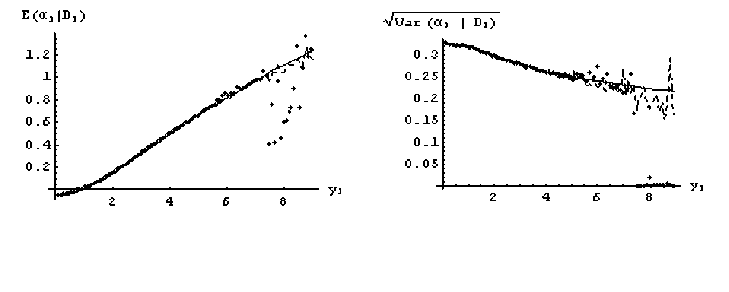
Figure 4: Comparison of particle filter procedures using the first and second order ap-
proximation to the log-likelihood function in a SV model. Left: mean evolution; Right:
standard deviation evolution; exact path (solid line); first order (dotted line); second order
(dashed line).

To better understand the infeasibility of using the first order APF to forecast the
variance evolution associated with stock returns within a standard SV model, we
present here a simple simulation that highlights the problems associated with the
existence of outliers. We illustrate these problems applied to update the distribution
of the first state, α₁ , in a standard SV model. It is supposed that α₀ follows a
Gaussian distribution with mean m0 and variance C0 . In the univariate model, the
updated distribution of α₁∖D₁, up to a normalizing constant c, has a known form

G.E.M.F - F.E.U.C.

<<   16   17   18   19   20   21   22   >>

More intriguing information