Second Order Filter Distribution Approximations for Financial Time Series with Extreme Outlier

J.Q. Smith and Antonio Santos

the particle filter procedure from the first period in all three sub-samples to both
algorithms and analysed the posterior distribution of each. A comparison was then
made between these distributions and the respective smoothing distribution.

In general, rudimentarily applied particle filter procedures have certain difficul-
ties in dealing with extreme observations. We therefore focused our attention on the
distributions of the states associated with extreme observations. Pitt and Shephard
(1999) applied the APF based on a first order approximation to the log-likelihood
function to some less challenging financial time series such as that representing the
evolution of the exchange rate of the Pound against the Dollar. However, stock
return series typically exhibit more extreme observations, so even the APF based
on a first order approximation to the log-likelihood starts to breakdown.

0       500      1000     1500

5

4

3

2

1

6

0     200   400    600   800   1000

4

2

0

6

4

2

0

0       500      1000     1500

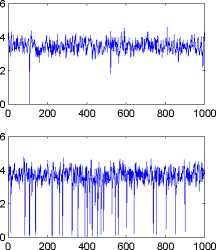
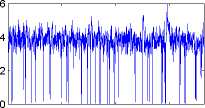
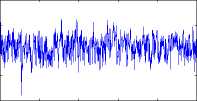
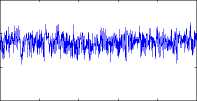
Figure 2: Difference between maximum and minimum value particles. Left-hand side:first
order filter;Right-hand side:second order filter. Each row corresponds to a different sub-
sample.

It can be seen that sample impoverishment for the APF, based on a first order
approximation particle filter applied to the series presented here, is sometimes ex-

G.E.M.F - F.E.U.C.

<<   14   15   16   17   18   19   20   >>

More intriguing information