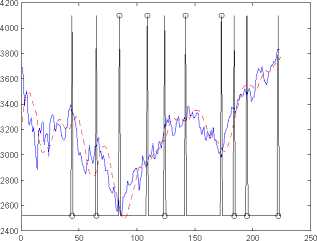
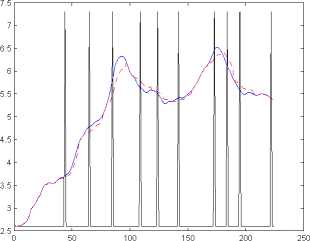
(a) Underlying (—), trend (--), prediction of abrupt (b) Risk-free ∆ tracking (—) and ∆ tracking (- -),
change locations (l) and their directions (o) prediction of abrupt change locations (l)
inria-00457222, version 1 - 16 Feb 2010
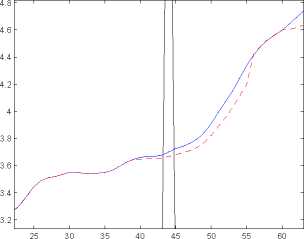
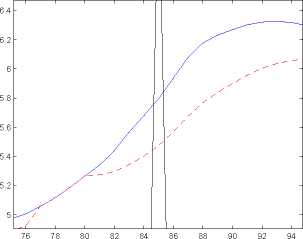
(c) Zoom on (b) (d) Zoom on (b)
Figure 4: Example 1 (continued): CFU9PY3500
[14] Fliess M., Join C., Sira-Ramirez H., Non-linear estimation is
easy, Int. J. Model. Identif. Control, 4, 12-27, 2008 (available at
http://hal.inria.fr/inria-00158855/en/).
[15] Garcia Coiiado F.A., d’Andrea-Novei B., Fliess M., Mounier
H., Analyse frequentielle des derivateurs algébriques, XXIIe Coll. GRETSI,
Dijon, 2009 (available at http://hal.inria.fr/inria-00394972/en/).
[16] Haug E.G., Derivatives: Models on Models, Wiley, 2007.
[17] Haug E.G., Taieb N.N., Why we have never used the Black-Scholes-
Merton option pricing formula, Working paper (5th version), 2009 (available
at http://ssrn.com/abstract=1012075).
[18] Huii J.C., Options, Futures, and Other Derivatives (7th ed.), Prentice
Hall, 2007.
[19] Kirkpatrick C.D., Dahiquist J.R., Technical Analysis: The Complete
Resource for Financial Market Technicians (2nd ed.), FT Press, 2010.
[20] Mandeibrot N., Hudson R.L., The (Mis)Behavior of Markets: A Frac-
tal View of Risk, Ruin, and Reward, Basic Books, 2004.
More intriguing information
1. Before and After the Hartz Reforms: The Performance of Active Labour Market Policy in Germany2. El impacto espacial de las economías de aglomeración y su efecto sobre la estructura urbana.El caso de la industria en Barcelona, 1986-1996
3. A Computational Model of Children's Semantic Memory
4. CHANGING PRICES, CHANGING CIGARETTE CONSUMPTION
5. The name is absent
6. The name is absent
7. The name is absent
8. On the origin of the cumulative semantic inhibition effect
9. The name is absent
10. The Structure Performance Hypothesis and The Efficient Structure Performance Hypothesis-Revisited: The Case of Agribusiness Commodity and Food Products Truck Carriers in the South