7 Appendix
7.1 Second-order conditions at the steady-state in the de-
centralized economy
To check, at the steady state, the second-order conditions of the problem of the firm
that guarantee the presence of a maximum it is possible to observe that we have (at
the steady-state):
∂ 2π
∂n2
∂2π
∂ (Td)2
∂ 2π
∂p2
α (α — 1) a [(1 - p) hTdL∖ 1-α 2 - ξ (ξ 1) (J p)' " nξ-2
-α (1 - α) A [(1 - p) hTdL∖ α 1 (1 - p)2 h2L2nα
-α (1 - α) A [(1 - p) hTdL∖ α 1 h2 (Td)2 L2nα +
nξ ■
-7 η
d L
(η - 1)(1 - p)θ pη-2 - θ (1 - p)θ-1 pη-1 +
-θ η (1 - p)θ-1 pη-1 - (θ - 1)(1 - p)θ-2 pη
∂ 2π
∂T d∂n
∂ 2π
∂ρ∂n
∂2π
∂n∂T d
= α (1 - α) A [(1 - p) hTdL] α (1 - p) hLnα-1
-α (1 - α) A [(1 - p) hTdL] α hTdLnα-1 +
∂ 2π
∂n∂p
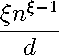
∂2π
∂T d∂p
∂ 2π
∂p∂T d
η (1 - p)θ pη-1 - θ (1 - pi"-' pη
: - (1 - α)2 A [(1 - p) hL]-α h (Td)-α Lnα
The hessian matrix is then:
|
■ ∂2π |
∂2π |
∂2π | |
|
∂n2 |
∂T d∂n |
∂ρ∂n | |
|
H = |
∂2π |
∂2π |
∂2π |
|
∂n∂T d |
∂(T d)2 |
∂ρ∂T d | |
|
∂2π |
∂2π |
∂2π | |
|
∂n∂ρ |
∂T d∂ρ |
∂ρ2 |
and in order to have a maximum for the problem of the firm the sequence of the
signs of the north-west principal minors of this matrix must be:
H1 < 0 H2 > 0 H3 < 0
With reference to this aspect we have:
H1 < 0 ⇒ ∣2∏ < 0 ⇒ α (α - 1) A [(1 - p) hTdL∖1-α nα-2- ξ (ξ - 1) (1 - p) p^ nξ-2 < 0
∂n2 d
28
More intriguing information
1. The name is absent2. 101 Proposals to reform the Stability and Growth Pact. Why so many? A Survey
3. CONSIDERATIONS CONCERNING THE ROLE OF ACCOUNTING AS INFORMATIONAL SYSTEM AND ASSISTANCE OF DECISION
4. Nurses' retention and hospital characteristics in New South Wales, CHERE Discussion Paper No 52
5. The Value of Cultural Heritage Sites in Armenia: Evidence From a Travel Cost Method Study
6. Policy Formulation, Implementation and Feedback in EU Merger Control
7. How Low Business Tax Rates Attract Multinational Headquarters: Municipality-Level Evidence from Germany
8. Human Rights Violations by the Executive: Complicity of the Judiciary in Cameroon?
9. Effort and Performance in Public-Policy Contests
10. The name is absent