allocate their demand across domestic goods in the same pattern, such that,
y(z)t = ppd^'- θ (cd + gd + mf * + cf * + gf *) (6)
where mf * = R01 p(z)t mf *(z)dz is the average demand for home country pro-
duced goods for use in foreign firms’ production. The demand for the firm’s
product depends upon its price relative to the prices of other domestic producers,
as well as the amount of domestic and foreign, public and private consumption
and intermediate good demand allocated to domestically produced goods where
these proportions depend on the relative prices detailed in (5). Therefore, we
are allowing for substitution in demand between goods produced at home and
abroad in describing the demand for the representative domestic firm’s product.
2.2 Imported Intermediate Goods
We now turn to consider the second channel through which we introduce open
economy effects into the firm’s pricing decision, by considering a production
function which includes imported intermediate goods as a factor of production,
y(z)t =
αNN (z)
f ρ-1∖ ρ-1 /ψ__1-ɪ
+ am(m(z)f) ρ K ψ
(7)
where N (z)t and m(z)tf are the labour input and imported intermediate goods
used in production. We model these inputs as imperfect substitutes and ρ
measures the elasticity of substitution between them. Firms also possess a stock
of capital, K, which is assumed, for simplicity, to be fixed and 1 — ψ describes
the weight given to capital in production. Here the first-order conditions for
cost minimisation are given by,
N(z)t = (y(z)t)ψ
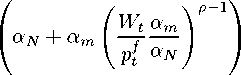
ρ-1
K ψ-1
(8)
and,
m(z)tf = (y(z)t)ψ
Wt am
ptf αN
1-ρ
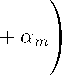
p — 1
(9)
which together reveal the cost-minimising combination of labour and interme-
diate goods,
N ( (z)tʌ = /
∖m(z)f} V
Wt αm
ptf αN
(10)