The name is absent

Now we state our solution concept.

Definition 2: Given a market game (U ( ),S ) , (x ,x ) with x =
-------------------- i i i∈I 1 i∈I

У x , x ∈ S ∀i ∈ I is said to be a Nash Equilibrium (N.E.) if Vi ∈ I
i∈I i i i

U (x , X ) ≥ U (x , X -X + X ) Vx ∈ S
i ɪ                          i i                       i i i i

Now we state and discuss our main assumptions.

1
Assumption 1: U ( ) ∈ G Vi ∈ I.
--------------------------------------- ɪ

*

Notice that under Assumption 1 (A.l in what follows) if ×_ι ∈ int. sɪ the
necessary condition of a N.E. reads as follows:

∂U (x*, x*)
i i
----------------- +

∂x
i

Let us define

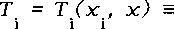
∂U
i

Let N be the set of active agents (i.e. those for which x* ∈ int. sɪ in a
N.E. with n players). N+l is defined accordingly. We will assume that N n N+l
≠ 0, i.e. at least one player is active in N.E. with n and n+1 agents
respectively.

Assumption 2: T (x , x) is strictly decreasing on x and x VieI.
----------------------------------------- i i                                                                                       i

12

<<   8   9   10   11   12   13   14   >>

More intriguing information