An alternative way to model merit good arguments

By definition of F^g (∙), F^g [x, y, u^g (z, x, y)] = z, which means the above expression
can be written as

From (14)

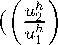
looks similar but has the extra term μ(y^h)).

For these preferences, it can be shown that the Marshallian demands for
commodity x is of the form

^db^h(q) - _χh

^χh(q, m^h) = χ^{h +} _b(_q^d)q^x- m. p [^mh - mh⁽p^)].               (⁴0)

where b(q ) is minimal expenditure necessary to generate one unit of utility and
m^h(p) =f z^h + q_xχ^h + q_yy^h denotes survival income. Similar expressions hold for
the other two commodities.

Under the lemma’s assumptions, expression (39) reduces for every agent h to

since the expression is homogenous of degree 0 in its arguments and the term
^m_q)-^jm(^p) thus drops out. Every agent will then have the same vector of (first best)

13

<<   11   12   13   14   15   >>

More intriguing information