12
Using (19) in (18) and simplifying, access value can be written as
AV œ "з±#з M8
#3
"з±#з m8 - x! /#3
#33 3
Mx /#3
M x "
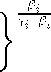
(20)
The Marshallian consumer's surplus approximation to access value is the integral
of the Marshallian demand over the interval (sp38,p38!),
AVQ
8
sp3
p38!
("3 - #3)e#!±!#4p4 ±"3M8“dp3
which, when integrated and simplified, can be expressed as
AVQ
œ χ! /#3 - " m8
3 3 #3

M8
M x "
(21)
TheDS Model with Two Constraints on Choice
The foregoing discussion developed the new DS system in terms of a money expenditure
function only, which is appropriate for standard money-constrained choice problems that
are used in most areas of demand analysis. When choice is constrained by time in
addition to money, as is likely with most recreational activities, a two-constraint version
of the model is needed. The properties of two-constraint choice models have been
discussed elsewhere (Bockstael, Hanemann, and Strand; Larson and Shaikh 2001). In
particular, Larson and Shaikh (2001) have identified the parameter restrictions on
demand systems that follow from the assumption that time is costly. It is straightforward
to show that the Marshallian demand system in (5) satisfies these conditions.
More intriguing information
1. SOME ISSUES IN LAND TENURE, OWNERSHIP AND CONTROL IN DISPERSED VS. CONCENTRATED AGRICULTURE2. The name is absent
3. Housing Market in Malaga: An Application of the Hedonic Methodology
4. The Variable-Rate Decision for Multiple Inputs with Multiple Management Zones
5. The name is absent
6. Commuting in multinodal urban systems: An empirical comparison of three alternative models
7. The Cost of Food Safety Technologies in the Meat and Poultry Industries.
8. The name is absent
9. Private tutoring at transition points in the English education system: its nature, extent and purpose
10. Delayed Manifestation of T ransurethral Syndrome as a Complication of T ransurethral Prostatic Resection