Stata Technical Bulletin
31
Population density

O Prey population (n) д Predator population (n)
900
800
700
600
500
400
900
800
700
600
500
400
Figure 3
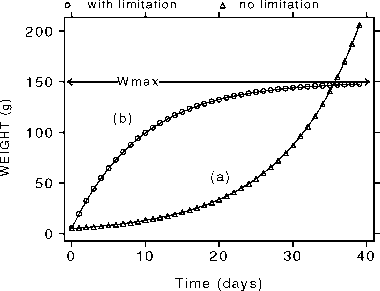
Figure 4
Figure 3 shows the simulations of the Volterra model of prey-predator interactions. In the top panel, no delay between predation and predator birth is
assumed. In the bottom panel, a time lag of 0.3 years is assumed to exist between predation and the new births. Figure 4 shows the growth process
of an organism, without limitations (a) and with a maximum value obtainable (b).

Figure 5
O Warm water flux (l/s)
2
(a)
Topt
1.5
1
5
cold water flux
15
.5
0
•30
•20
10
50
30
20
10
0
2
4
6
8
10 12
S Shower water temperature
50
•40 1.5
1
.5
0
•50 2
40
30
20
10
0
2
4
6
8
10 12
2
40 1.5
1
.5
0
50
40
30
20
10
0
2
4
6
8
10 12
Figure 6
Time (s)
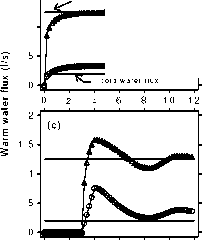
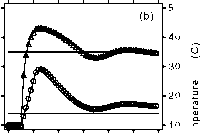
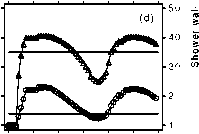
Figure 5 shows the growth process of an organism, switch-off (a) and switch-on (b) effects of the SWTC function. Figure 6 shows the shower water
temperature regulation: a) perfect (no delay); b) long pipe (constant information delay); c) long pipe (information delay, variable as a function of total
flux); d) lizard adjusting (material delay, variable as a function of the mixed water temperature).
References
ACSL. 1987. Advanced Continuous Simulation Language, User Guide/Reference manual, Edition 4.1. Concord, MA: Mitchell and Gauthier Assoc.
Brennan, R. D., C. T. De Wit, W. A. Williams, and E. V. Quattrin. 1970. The Utility of a Digital Simulation Language for Ecological Modeling.
Oecologia (Berlin) 4: 113-132.
Dent, J. B. and M. J. Blackie. 1979. System Simulation in Agriculture. London: Applied Science Publishers.
de Wit C. T. and J. Goudriaan. 1978. Simulation of ecological processes. Wageningen: PUDOC.
Ferrari, T. J. 1978. Elements of System-Dynamics Simulation—A textbook with exercises. Wageningen: PUDOC.
Forrester, J. W. 1968. Principles of Systems. Cambridge: MIT Press.
More intriguing information
1. A MARKOVIAN APPROXIMATED SOLUTION TO A PORTFOLIO MANAGEMENT PROBLEM2. The Making of Cultural Policy: A European Perspective
3. The name is absent
4. The Impact of Minimum Wages on Wage Inequality and Employment in the Formal and Informal Sector in Costa Rica
5. The name is absent
6. REVITALIZING FAMILY FARM AGRICULTURE
7. he Virtual Playground: an Educational Virtual Reality Environment for Evaluating Interactivity and Conceptual Learning
8. AJAE Appendix: Willingness to Pay Versus Expected Consumption Value in Vickrey Auctions for New Experience Goods
9. Nach der Einführung von Arbeitslosengeld II: deutlich mehr Verlierer als Gewinner unter den Hilfeempfängern
10. Thresholds for Employment and Unemployment - a Spatial Analysis of German Regional Labour Markets 1992-2000