Stata Technical Bulletin
13
metatrim first calls program meta to perform and report a standard meta-analysis of the original data, showing both the
fixed- and random-effects results. These initial results are always reported as theta estimates, regardless of whether the data were
provided in exponentiated form.
metatrim next reports the trimming estimator and type of meta-analysis model to be used in the iterative process, then
displays results at each iteration. The estimate column shows the value of Δ^ at each iteration. As expected, its value at
iteration 1 is the same as shown for the random-effects method in the meta-analysis panel, and then decreases in successive
iterations as values are trimmed from the data. Column Tn reports the Tn statistic, column # to trim reports the successive
estimates feθŋ and column diff reports the sum of the absolute differences in signed ranks between successive iterations. The
algorithm stops when diff is zero.
metatrim finishes with a call to program meta to report an analysis of the trimmed and filled data. Observe that there
are now 36 studies, composed of the n = 29 observed studies plus the additional ко = 7 imputed studies. Also note that the
estimate of Δ reported as the random effects pooled estimate for the 36 studies is not the same as the value Δ%) shown in
the fifth (and final) line of the iteration panel. These values usually differ when the random-effects model is used (because the
addition of imputed values change the estimate of τ2) but are identical always when the fixed-effects model is used.
In summary, metatrim adds 7 “missing” studies to the dataset, moving the random-effects summary estimate from
Δ = 0.716,95% CI: (0.595,0.837) to Δ = 0.655,95% CI: (0.531,0.779). The new estimate, though slightly lower, remains
statistically significant; correction for publication bias does not change the overall interpretation of the dataset. Addition of
“missing” studies results in an increased variance between studies, the estimate rising from 0.021 to 0.031, and increased evidence
of heterogeneity in the dataset, p = 0.118 in the observed data versus p = 0.054 in the filled data. As expected, when the
trimmed and filled dataset is analyzed with the publication bias tests of Begg and Mazumdar and Egger et al. (not shown),
evidence of publication bias is no longer observed (p = 0.753 and p = 0.690, respectively).
The funnel plot (Figure 1), requested via the funnel option, graphically shows the final filled estimate of Δ (as the horizontal
line) and the augmented data (as the points), along with pseudo confidence-interval limits intended to assist in visualizing the
funnel. The plot indicates the imputed data by a square around the data symbol. The filled dataset is much more symmetric than
the original data and the plot shows no evidence of publication bias.
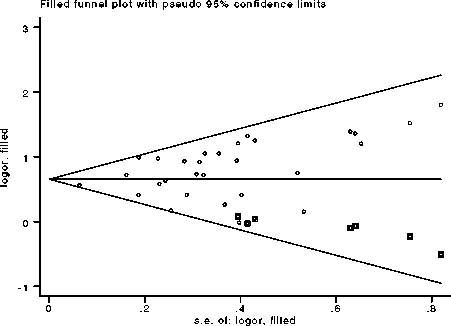
Figure 1. Funnel plot for analysis of Cottingham and Hunter data.
Additional options that can be specified include print to show the weights, study estimates and confidence intervals for
the filled data set, eform to request that the results be reported in exponentiated form in the final meta-analysis and in the
print option be reported in exponentiated form (this is useful when the data represent odds ratios or relative risks), graph to
graphically display the study estimates and confidence intervals for the filled data set, and save fifilnamee) to save the filled data
in a separate Stata datafile.
Remarks
The Duval and Tweedie method is based on the observation that an unbiased selection of studies that estimate the same
thing should be symmetric about the underlying common effect (at least within sampling error). This implies an expectation that
the number of studies, and the magnitudes of those studies, should also be roughly equivalent both above and below the common
effect value. It is, therefore, reasonable to apply a nonparametric approach to test these assumptions and to adjust the data until
the assumptions are met. The price of the nonparametric approach is, of course, lower power (and a concomitant expectation
that one may under-adjust the data).
More intriguing information
1. Portuguese Women in Science and Technology (S&T): Some Gender Features Behind MSc. and PhD. Achievement2. Death as a Fateful Moment? The Reflexive Individual and Scottish Funeral Practices
3. Impacts of Tourism and Fiscal Expenditure on Remote Islands in Japan: A Panel Data Analysis
4. Innovation in commercialization of pelagic fish: the example of "Srdela Snack" Franchise
5. The name is absent
6. The name is absent
7. Delivering job search services in rural labour markets: the role of ICT
8. Philosophical Perspectives on Trustworthiness and Open-mindedness as Professional Virtues for the Practice of Nursing: Implications for he Moral Education of Nurses
9. THE EFFECT OF MARKETING COOPERATIVES ON COST-REDUCING PROCESS INNOVATION ACTIVITY
10. Qualifying Recital: Lisa Carol Hardaway, flute