Mean Variance Optimization of Non-Linear Systems and Worst-case Analysis

L_m = L1 + L2 =

l-γ

^r1^L

1^N

-1 X

N ʌ

j=1

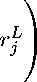
+ L-γ

1^N

-1 X rL
vʌ ^j
j=1

(27)

and L_c is given by (2). The first order conditions are then given by

∂ ■               ∂LL1 ɪ L L ^L2_

_l L = ^Lh ⁺ (^r1 ^- cm) ^TΓL ⁺ (^r2 ^- cm) ^TΓL = 0 for ^h = 1, ²

∂r_h                   ∂r_h             ∂r_h

(28)

—c = L_c + (r_iL — c_c)    = 0 for i = 3...N.

∂r^{L     c i c} ∂r^{L                ... .}

(29)

We look at the post-merger equilibrium where r₁^L = r₂^L = r_m^L and r_i^L = r_c^L . Substituting

(27) in (28) and (2) in (29), we obtain the best response functions as

_L l cm r^L
_rL =---._r „ + — + -c-
^m   2γ( ⁿN² )    ^{2    2}

(30)

_L l N—1      2 _L

r^c = γ( N+1 )⁺( N + 1)c^{c +} N + 1 rm.                    (³¹)

Solving (30) and (31) gives the post-merger equilibrium loan rates r_m^L and r_c^L . Substituting
r_m^L and r_c^L respectively in (27) and in (2) gives the equilibrium L_m and L_c. Analogously, we
derive Dm and Dc.                                                          Q.E.D.

Proof of Corollary 3

33