Mean Variance Optimization of Non-Linear Systems and Worst-case Analysis

Differentiating (18) with respect to R_m gives

From (17) it follows ^d(^ωma~^ωms) > 0 for Rm < Dm and ^d(^ωm^a-^ωm^s) < 0 otherwise. This,
dR_m                  2         dR_m

along with ω_ma - ω_ms =0 both for R_m = 0 and for R_m = D_m implies ω_ma - ω_ms > 0for

all Rm ∈ [0,Dm].                                                               Q.E.D.

Proof of Proposition 2

The demand for liquidity of the merged banks, x_m = δ₁ Dm + δ2 Dm, has density function

as in (16). Using Leibniz’s rule, the equality D_m = R_m + L1 + L2, and the ratio k_m

from (11) we can express the first order condition dRm = 0 as

8 km - 4km + 1 = ^rD for km ≤ 1/2

8(1 - km)3 = ^rD      for km > 1/2.

The term on the LHS of the equalities is the marginal benefit of increasing the reserve-
deposit ratio, that is the reduction in the expected need of refinancing induced by a marginal
increase of the reserve ratio. The term on the RHS of the equalities is the ratio between the
marginal cost of raising reserves r^D and the marginal cost of refinancing r^I. From (19), we
obtain:

k_m

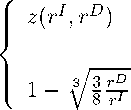
for r^I ≤ 3r^D

for r^I > 3r^D,

(20)

where z(rI, r^D) is the solution of the equation z³ — 3z² + 8(1 — ^rD) = 0 in the interval (0, ∣]
increasing in the ratio rD. Since f(0) > 0, f(1/2) < 0 and f⁰(z) < 0, z(rI,r^D) is the unique
real solution.

To compare km with ksq, we rearrange ksq given in (10) as

r^D

^{(1 - k}sq) = r∣γ-,                                       ⁽²¹⁾

where, as before, the LHS is the marginal benefit of increasing the reserve-deposit ratio and
the RHS is the ratio between the marginal cost of raising deposits and holding reserves r^D
and the marginal cost of refinancing r^I .

31

<<   30   31   32   33   34   35   36   >>

More intriguing information