JJexp(2 i π j 1 x )exp(2 i π j 2 y )min(x, y ) dxdy
x
= ∣exp(2 i π j 1 x)ʃy exp(2 i π j2y)dydx - ∣x exp(2 i πj 1 x)∣exp(2 i π j2y)dydx
x exp(2 iπ (j'i +j2)x) ʃ exp(2 iπ (j'i +j2)x) ʃ exp(2 iπ ji x)
______________dx ʃ I__________LJ___dx + I_________1__dx
(A.42)
2 i π j 2 2 (2 i ∏ j 2)2 2 (2 i π j 2)2
ʃx exp(2 iπ (j' 1 +j2) x) ʃxexp(2 iπ j 1 x)
- I____________LJ___dx + I___________1__dx
2 2 i π j 2 2 2 i π j 2
= _ 1 + 1(j' 1+j 2=0)
4 π 2j 12 4 π2j 2
and
x
∣exp(2 i π j 1 x)∣exp(2 i π j2y)dydx ʃ ʃ
0
exp(2 iπ (j' 1 +j2) x)
2 i π j 2
dx -
exp(2 i π j 1 x )
2 i π j 2
dx
I(j-1÷j 2=0)
2 i π.j,
(A.43)
It follows now from (A.38) and (A.42) that
ʃʃ':(x)Fm(y)min(x,у)dxdy = —2 Σ
jj 4π2 j≠0
( V
j2
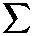
Λj
4π2
Ij-1
cc
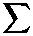
∞
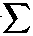
j-i
A
Ï
c....
Ï
c_..„
(A.44)
ʌ Vλ β j,kβ j,
2^t 2 2
j=1 j
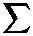
V
∞
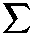
λ.1
A
. A
βjm
and it follows from (A.38) and (A.43) that
ʃFk(x )fFm (У ) dydx = ɪ Σ cjk-j
0 ∙0 2 i π j≠0 j
« jkβ j
1 τL « ∙t∣
= ⅛∑ —
4π
Moreover,
45
A
j « β t
Γλ j, mtJ,k
j=1
(A.45)
More intriguing information
1. Political Rents, Promotion Incentives, and Support for a Non-Democratic Regime2. Financial Development and Sectoral Output Growth in 19th Century Germany
3. Transgression et Contestation Dans Ie conte diderotien. Pierre Hartmann Strasbourg
4. The name is absent
5. For Whom is MAI? A theoretical Perspective on Multilateral Agreements on Investments
6. 101 Proposals to reform the Stability and Growth Pact. Why so many? A Survey
7. Social Balance Theory
8. The name is absent
9. The name is absent
10. HEDONIC PRICES IN THE MALTING BARLEY MARKET