m
∑v*v* T
XkXk
k= 1
- λRTC(1)C(1) RJ"
= 0,
(A.50)
where the X*i’s are i.i.d. Nq-r(0,Iq-r), and the latter minimum solution is equal to, and bounded
from below by
inf
m
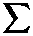
LM
η η tR C(1)C(1)TRqJ"η
m
inf__lm_______
η η Tη
infη TRqTrC (1) C (1) TRrrη
η η Tη
(A.51)
m
кk1
ï
T λ. RTC(1)C(1)TR, ).
mιn∖ q r v 7 V 7 ,q-rf
7
This proves the inequality involved. Since
m +1
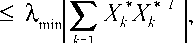
V
√
(A.52)
and Mα,s,q-r,m is decreasing in m, it follows now that the right-hand side lower bound involved
increases with m. Q.E.D.
Proof of Lemma 8: For k > 0 we can write
n
(A.53)
2J2 t cos(2kπ (t-0.5)/n) = gn(2kπ /n) + gn(-2kπ /n),
where
47
More intriguing information
1. Critical Race Theory and Education: Racism and antiracism in educational theory and praxis David Gillborn*2. Infrastructure Investment in Network Industries: The Role of Incentive Regulation and Regulatory Independence
3. AGRICULTURAL PRODUCERS' WILLINGNESS TO PAY FOR REAL-TIME MESOSCALE WEATHER INFORMATION
4. ¿Por qué se privatizan servicios en los municipios (pequeños)? Evidencia empírica sobre residuos sólidos y agua.
5. Should Local Public Employment Services be Merged with the Local Social Benefit Administrations?
6. CONSUMER ACCEPTANCE OF GENETICALLY MODIFIED FOODS
7. AN EMPIRICAL INVESTIGATION OF THE PRODUCTION EFFECTS OF ADOPTING GM SEED TECHNOLOGY: THE CASE OF FARMERS IN ARGENTINA
8. Literary criticism as such can perhaps be called the art of rereading.
9. The name is absent
10. Land Police in Mozambique: Future Perspectives