Large-N and Large-T Properties of Panel Data Estimators and the Hausman Test

and the correlations between x_3,it and z_i no longer play any important role in
asymptotics. Assumption 6(iii) rules out such cases.

Assumption 6 is about the asymptotic properties of means of regressors
as T →∞. We also need additional regularity assumptions on the means of
regressors that apply as N →∞.Define

= τ 1(r)dr;

H32 =

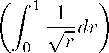
Ik32 ; H33 =

τ 33(r)dr;

and

H32g32,i (zi)

H33g33,i (zi)
zi - Ezi

H32g32,i (zi)

H33g33,i (zi)
zi - Ezi

Γ
g32,g32,i

Γ⁰

g32, g33,i

_Γ0 _i

Γ
g32,g33,i

Γ
^g33^,g33^,i

With this notation, we assume the followings:

Assumption 7 (convergence as N →∞):

^θ21,i = ^θ21,i ^- N Pi ^θ21,i; ^μg32,i = ^μg32,i ^- N Pi ^μg32,i
ɪ P∙ μ_n . As N →∞,

N iμ ^μg33,i ^,

Define Θ1,i = Θ1,i -

; and ^μg33,i

NN ∑i θι,i;
= ^μg33,i ^-

H1θ1,i H1θ1,i

(i) N∑i

θ21,i θ21,i

H³2^μg32,i H³2^μg32,i

WJ WJ

ΓΘ1,Θ1
Γ⁰Θ1,Θ21
Γ

' Θ.,μ 2

VKμ33

ΓΘ1,Θ21

^ΓΘ21^,Θ21

Γ⁰

^θ21^,μ32

Γ⁰

^θ21^,μ33

^r^θ1^,μ32
^rθ21,μ32
Γ

^μ32,^μ32

Γ⁰

μ32^,g33

^r^θ1^,μ33
^r‰^,μ33
Γ

^μ32,^μ33

^μ μ33^,μ33/

^Γg32,g32,i

(ii) NN∑ -

g32, g33, i

g33,g33,i

_Γ0 _i

(iii) The limit of ɪ Pi θɪ,iΘ1,_i

Γg32,z,i Γg32,g32

Γg33,z,i → Γ⁰g₃₂ ,g₃₃

Γzz,i Γg₃₂,z

exists.

g32^,g33

g33,g33

Γ⁰

^g33^,z

g32,z

g33,z

Γ
z,z

Apparently, by Assumptions 6 and 7, we assume the sequential convergence
of the means of regressors as T → ∞ followed by N →∞. However, this by
no means implies that our asymptotic analysis is a sequential one. Instead, the
uniformity conditions in Assumption 6 allow us to obtain our asymptotic results
using the joint limit approach that applies as (N, T → ∞) simultaneously.¹⁶Joint limit results can be obtained under an alternative set of conditions that
assume uniform limits of the means of regressors sequentially as N → ∞ followed
by T →∞. Nonetheless, we adopt Assumptions 6 and 7, because they are much
more convenient to handle the trends in regressors x_1,it and x_3,it for asymptotics.

The following notation is for conditional or unconditional covariances among
time-varying regressors. Define

Γi (t, s) = [Γjl,i (t, s)]jl,

¹⁶ For the details on the relationship between the sequential and joint approaches, see Apos-
tol (1974, Theorems 8.39 and 9.16) for the cases of double indexed real number sequences,
and Phillips and Moon (1999) for the cases of random sequences.

More intriguing information

1. The name is absent
2. Flatliners: Ideology and Rational Learning in the Diffusion of the Flat Tax
3. DEVELOPING COLLABORATION IN RURAL POLICY: LESSONS FROM A STATE RURAL DEVELOPMENT COUNCIL
4. FUTURE TRADE RESEARCH AREAS THAT MATTER TO DEVELOPING COUNTRY POLICYMAKERS
5. Detecting Multiple Breaks in Financial Market Volatility Dynamics
6. Wirtschaftslage und Reformprozesse in Estland, Lettland, und Litauen: Bericht 2001
7. Public Debt Management in Brazil
8. Visual Perception of Humanoid Movement
9. Investment in Next Generation Networks and the Role of Regulation: A Real Option Approach
10. Julkinen T&K-rahoitus ja sen vaikutus yrityksiin - Analyysi metalli- ja elektroniikkateollisuudesta