Large-N and Large-T Properties of Panel Data Estimators and the Hausman Test

N¹ X EFzi kRiTk
i

≤ sup EFz_i kRiT k ≤ sup EFz_i kQiTk1{kQiTk >M}.       (39)

N X(PiT ^- EFz_i PiT )
i

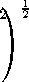
(⅛ X EFzi ° PiT ^- EFZi PiT ° ²2

≤√⅛ μsi^uτp EFzi ^kPiT k²)²

≤

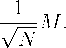
(40)

Choose M = N a, where 0 < a < 2. Then, (39) , (40) → 0 α.s.. Consequently,
we have (38). ¥

Lemma 15 Suppose that Assumptions 1-8 hold. Let F_z^∞ = σ (z1, ..., zN , ...) .
For a generic constant M that is independent of N and T, and for some F_z^∞ -
measurable function M_z , the followings hold:

(a) ^suPi,τ TT Pt (xι,it ^- Exι,it) °₄ < M;

(b) ^suPi,T √T Pt (^χ2,it ^- E^χ2,it) ∣∣₄ < M;

(^c) ^suPi,T √1T Pt (^χ3,it ^- EFz_i^χ3,i0 °F 4 < Mz^, a.s.;

(^d) ^suPi,T ° √T Pt (^χ3,it ^- EFz_i ^χз,it¢ ∣∣₄ < M.

Proof

We here use q to denote the real number used in Assumptions 1-6, which is
strictly greater than 1.

Part (a)

Note that

≤ sup kx1,it - Ex1,itk₄

i,T

≤ sup kx1,it - Ex1,itk_4q = κx₂ < ∞,
i,T                      ^q

where the first inequality holds by Minkowski’s inequality, the second inequality
holds by Liapunov’s inequality, and the last inequality holds by Assumption 2.
Choose M = κ_x2 . ¥

Part (b)

34

<<   31   32   33   34   35   36   37   >>

More intriguing information