4 ∖4 1 T-1 s s Q-1
4!8 f sup ∣∣Xit∣∣4qj sup T∑∑∑α,(s) q
, i,T s=1 p=0 k=0
4∞ 1
sup ∣Xit ∣4q X(s +1)2 sup ai (s) q < M,
(43)
i,t s=1 i
where the last bound holds because supi ai (s) is of size —3 ^-ɪ (see Assumption
3(i)). By the similar fashion, we can also show that
II,III,IV ≤ 4!8
4∞
sup∣Xit∣4q (
i,t s=1
s +1)2 sup αi (s) q <M,
i
and we have all the required result. ¥
Part (c)
Let Yit = xh,3,it — EFz xh,3,it. Using the arguments similar to those used in
the proof of Part (b), we can show that under Assumption 4,
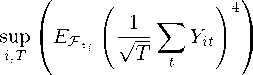
2M (sup kYitkFzi,4q) X s2 (sup aFzi (s) qq )
a.s.,
(44)
for some constant M. By Assumption 4(i), P∞= s2 supi aFZ (s) q < ∞ a.s..
Finally, since the terms supi t kYitkF 4q and PS=1 s2 supi αFz. (s) q are F∞o-
measurable, we have the desired result by choosing
Mz =2M
sup kYitk4Fzi,4q Xs2 sup aFzi
q— 1 ∖
(s) ~ J . ¥
Part (d)
Again, let Yit = xh,3,it — EFzi xh,3,it. From (44) , we have
sup
i,T
Yit
sup E
i,T
Yit
≤ 2ME
(sup kYit ∣Fzi ,4q) X s2 (sup aFzi (s) q—q~ ɔ
≤ 2M E
sup kYitk8Fzi,4q
)]2 E{ x s2('
36
q — 1
sup αFzi (s) q
(45)
More intriguing information
1. Geography, Health, and Demo-Economic Development2. The name is absent
3. Higher education funding reforms in England: the distributional effects and the shifting balance of costs
4. Individual tradable permit market and traffic congestion: An experimental study
5. Lending to Agribusinesses in Zambia
6. The Formation of Wenzhou Footwear Clusters: How Were the Entry Barriers Overcome?
7. Developmental changes in the theta response system: a single sweep analysis
8. Weak and strong sustainability indicators, and regional environmental resources
9. The name is absent
10. Are Public Investment Efficient in Creating Capital Stocks in Developing Countries?