It follows that
TN~Nv(b(Bb - B)
= T √Nvec
NT
XXyi(,2t)-1yi(,2t)-10
i=1 t=1
-1
NT
X X (2) v0
yi,t-1vit
i=1 t=1
-→ N(0, Ω-1 ® Σv ) .
! ■---^ !
Finally, it is easy to verify that if αbi-αi = Op(T-1/2) and Σb i-Σi = Op(T-1/2)
we have
NT NT
T ∑ ∑ yg - 1 V0t = t√n ∑∑ УЗ-1 vit + op (1)
i=1 t=1 i=1 t=1
and, thus, replacing αi and Σi by a consistent estimator does not affect the
asymptotic distribution.
Proof of Theorem 2
First, assume that αi and β (and therefore αi,⊥ and β⊥) are known. The
vector of regressors results as
wi
β⊥yz,t-1 = β⊥β⊥(α)-1 αi,⊥ XX . + Op(T1 /2)
s=1
ΓSi,t-1 + op(T1/2) ,
where Sit = Pts=1 α0i,⊥εis and Γ = β⊥0 β⊥ (α0i,⊥β⊥)-1 . Accordingly, under the
null hypothesis α0i,⊥∆yit = αi0,⊥εit the respective Wald statistic can be written
as
λiw(r)
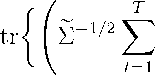
× XT ΓSi,t-1∆Si0t
t=1
∆Sit Si0,t-1Γ0 Xt=T1 ΓSi,t-1Si0,t-1Γ0
-1
∑ -1 / 2} + Op (1)
tr½∑-1 /2 (∑∆SitSit-ə (∑Sit-1 S0,t-1
-1
X
=1
Si,-1∆Si0t
∑ -1 / 2} + Op (1)
where Σ 1 /2 is a symmetric matrix with the property Σ 1 /2Σ 1 /2 = α'i ⊥Σαi,⊥.
It remains to show that the limiting distribution is not affected if β⊥ and
16