Theorem 2: Let yt be generated by a VAR(1) process with EC representation
(1) and 0 ≤ r < k - 1. Furthermore εit and εjt are independent for i 6= j. Let
bi,⊥ and β⊥ be √T-consistent estimates for some orthogonal complements of
αi,⊥ and β⊥, respectively. If T → ∞ is followed by N → ∞ we have
√N ( λr — μr )
σr
-→ N(0, 1) ,
where
μr
E[λi (r)]
E tr
dWk-rWk0-r
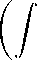
Wk-rWk0-r -1 Wk-rdWk0-r
E tr [ λi ( r ) — μr ]2
var
tr Z
dWk-rWk0-r
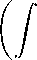
Wk-r Wk0-r -1 Wk-rdWk0-r
λ(r) = N 1 Pn=1 λi (r) and λi (r) denotes the LR, Wald or LM statistic of
the hypothesis δi = 0 in the regression
ubit = δi0wbi,t-1 + eit , t = 1, . . . , T , (9)
.—.
where ubit = αb0i,⊥∆yit and wbit = β⊥0 yit .
A convenient (Wald type) test statistic of the null hypothesis is
T T -1 T T
λiW (r) =Ttr
vitwi0,t-1 wi,t-1wi0,t-1 wi,t-1vi0t vitvi0t
t=1 t=1 t=1 t=1
The values μr and σ2 are computed by Lyhagen et al. (2001) for the model
without deterministic terms.
Hypotheses on the cointegration parameters can be tested by using a LR
statistic. Following Johansen and Juselius (1994) we consider the following
class of linear hypotheses on the cointegration vectors:
H0 : β= [β1,...,βr] = [Φ1θ1,...,Φrθr] , (10)
where Φj is a known k × qj matrix with 1 ≤ qj ≤ k — r and θj is a qj × 1
vector for j = 1, . . . , r . Note that for the identification of the cointegration
vectors r normalization restrictions are required so that the maximal number