5th and 8th grade pupils’ and teachers’ perceptions of the relationships between teaching methods, classroom ethos, and positive affective attitudes towards learning mathematics in Japan

254

Table 7.4.9: Mean s∞res and Standard Deviation of teachers’ perceptions of the extent
to which they praise their pupils in mathematics classes
f-th____I _ ɪ___L

Figure 7.4.3: Mean scores of pupils’ perceptions of the extent to which mathematics
teachers praise pupils (age group comparison)

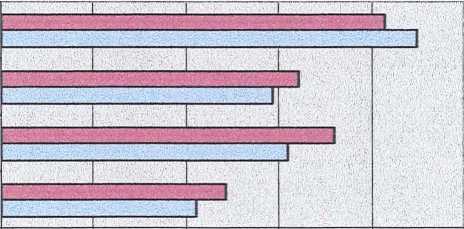
□ 8th grade
teachers

θ5th grade
teachers

0         1         2         3         4        5

I=Better results than others, 2=lmprovement results than before,
3=More effort than others, 4=More effort than before

5^th grade teachers, overall, who gave result-based praise were likely to do so based on
both relative comparisons and absolute comparisons (r=. 464, p=. 001). 8^th grade
teachers seemed to praise their pupils in an integrated way. There were positive
Comelations ranging from r=. 423 to r=. 671, between the various types of praise used.

The relationships between teachers’ reported frequency of adoption of praise and their
perceptions of the effects and deployment of different teaching methods were not
examined, due to the skewed distribution of responses. 10.6% of 5^th grade teachers and
19.0% of 8^th grade teachers replied that they always or nearly always praised pupils for

254

<<   265   266   267   268   269   270   271   >>

More intriguing information