2.1. Theoretical basis
MISEP is an extension of the well known INFOMAX method
[9]. Figure 1 Shows the general structure of the network
that is used. The module that performs the ICA operation
proper is marked F in the figure (in INFOMAX this module
performs simply a product by a matrix, while in MISEP it
generally is a nonlinear module). The result of the analysis
are the components yi . The ψi modules, and their outputs
zi, are auxiliary, being used only during the training phase.
Each of those modules applies an increasing function, with
values in [0, 1], to its input.
o1
o2
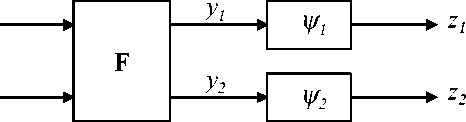
Fig. 1. Structure of the ICA systems studied in this paper. In the
INFOMAX method the nonlinearities ψi are fixed a-priori. In the
MISEP method they are adaptive, being implemented by MLPs.
Assume that each of these functions is the cumulative
probability function (CPF) of the corresponding input yi . In
such a case it’s easy to see that each zi will be uniformly
distributed in [0, 1]; therefore H (zi) = 0, and
I(z)=XH(zi)-H(z)=-H(z). (3)
i
On the other hand, since each of the zi is related to the cor-
responding yi through an invertible transformation, I(y) =
I(z). Consequently
I(y) = -H(z). (4)
If we maximize the output entropy we shall, therefore, be
minimizing the mutual information I(y), as desired. Both
INFOMAX and MISEP learn by maximizing the output en-
tropy.
In INFOMAX the F module is linear, as said above, and
the nonlinearities ψi are fixed, being chosen by the user. In
the framework of the reasoning given in the previous para-
graph, this corresponds to an a-priori choice of the estimates
of the CPFs of the components to be extracted. Linear ICA
is a rather constrained problem, and even relatively poor ap-
proximations of the actual CPFs work well in many cases.
MISEP extends INFOMAX in two ways: (1) the ICA
module F is generally nonlinear, to allow the system to per-
form nonlinear ICA, and (2) the ψi modules are adaptive,
learning the estimates of the CPFs during the training pro-
cess. Having good estimates of the actual CPFs is important
for MISEP, because nonlinear ICA is much less constrained
than its linear counterpart. Consequently, poor CPF esti-
mates can easily lead to poor ICA results.
One of the main ideas behind MISEP is that, by max-
imizing the output entropy H (z), we can simultaneously
achieve two objectives: (1) we lead the adaptive nonlineari-
ties ψi to become estimates of the CPFs of their respective
inputs and, this being so, (2) we minimize the mutual infor-
mation I(y), because in such a situation I(y) = -H (z), as
shown above. To see that we achieve objective (1), assume
for the moment that the F module was fixed. Then I(y) and
I(z) would be fixed. From (3)
H(z)=XH(zi)-I(z). (5)
i
This shows that maximizing H(z) would lead to the indi-
vidual maximization of each of the H(zi) (since they are
decoupled from one another). The maximum of H(zi) will
correspond to a uniform distribution of zi in [0, 1], if the
function ψi is constrained to have values in [0, 1]. If this
function is also constrained to be increasing, it will equal
the CPF of yi at that maximum. We see, therefore, that if
we constrain the ψi modules to yield increasing functions
with values in [0, 1], they will estimate the CPFs of their
inputs.
2.2. Implementation
The MISEP method can be implemented in different ways,
and this paper discusses two different implementations: in
this section we briefly describe the previous implementa-
tions, in which both the F and the ψi modules were based on
multilayer perceptrons (MLPs); the next section discusses
implementing the F module by means of a radial basis func-
tion (RBF) network.
There are two main issues in the implementation MISEP:
training the F and ψi modules according to a criterion of
maximum output entropy H(z), and constraining the ψi
modules as described in the previous section. Both the train-
ing and the constraints issues are discussed in detail in the
references, e.g. [8].
Briefly speaking, the constraints on the ψi blocks are
implemented by using linear output units , normalizing the
Euclidean norms of the weight vectors of these units, and
initializing all weights of these modules to positive values.
Training of the network of Fig. 1 is done through gra-
dient descent. The objective function is first transformed as
follows:
H(z) =H(o)+hlog|detJ|i (6)
where J = ∂z/∂o is the Jacobian of the transformation
performed by the network, and the angle brackets denote
expectation. The entropy H(o) doesn’t depend on the net-
work’s parameters, and can be ignored in the optimization.
The other term on the right hand side of this equation is