FASTER TRAINING IN NONLINEAR ICA USING MISEP

1

0.5

0

-0.5

-1

-1.2     -1     -0.8    -0.6    -0.4    -0.2      0      0.2     0.4     0.6     0.8

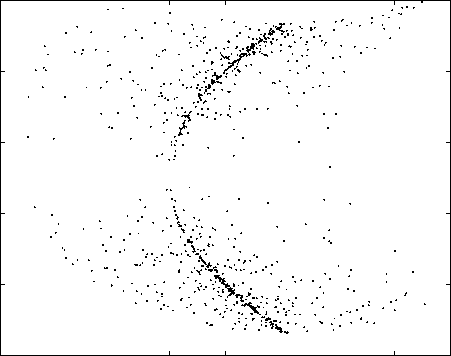
Fig. 4. Separation performed by the MLP-based network.

0.1
0.08
0.06
0.04
0.02

0
-0.02
-0.04
-0.06
-0.08
-0.1

-0.06      -0.04      -0.02         0         0.02        0.04        0.06        0.08        0.1

Fig. 6. Mixture of a supergaussian and a subgaussian source.

1.5

1

0.5

0

-0.5

-1

-1.5

-1.5

-1

-0.5

0.5

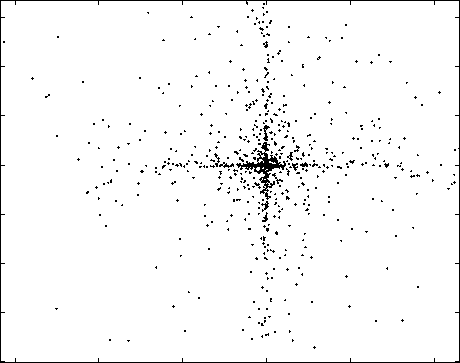
Fig. 5. Separation performed by the RBF-based network.

1

-1

-1.5

-0.4     -0.3     -0.2     -0.1       0       0.1       0.2      0.3      0.4      0.5      0.6

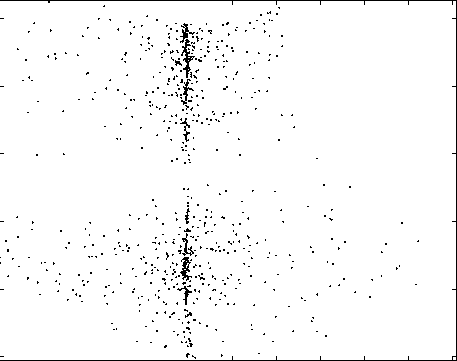
Fig. 7. Separation performed by the MLP-based network.

slow training of MLP-based nonlinear ICA systems is the
nonlocal character of these networks.

Figure 9 shows an example of an ICA result obtained
with the RBF-based network, in the case of the mixture of
two supergaussians, but without weight decay. While a rel-
atively good ICA result was achieved (the estimated mutual
information is the same as in Figs. 4 and 5), the original
sources were not separated. This shows the importance of
using regularization with networks of this kind.

5. CONCLUSIONS

We have briefly presented the MISEP, a method for linear
and nonlinear ICA, which is an extension of the well known
INFOMAX method. We discussed a possible cause for the
relatively slow learning that it sometimes shows, having
conjectured that it was due to the use of non-local units in
the network that performs the ICA operation.

This conjecture was confirmed by experimental tests, in
which a system based on a radial basis function network was
compared to one based on a multilayer perceptron on the
same nonlinear ICA problems. These tests confirmed that
that system based on RBF units learns significantly faster,
and shows a lower variability of the training times. The tests
also showed, however, that the RBF-based system needs to
have explicit regularization to be able to perform nonlin-
ear source separation, contrary to what happened with the
MLP-based one.

<<   2   3   4   5   6   >>

More intriguing information