FASTER TRAINING IN NONLINEAR ICA USING MISEP

0.1
0.08
0.06
0.04
0.02

0
-0.02
-0.04
-0.06
-0.08

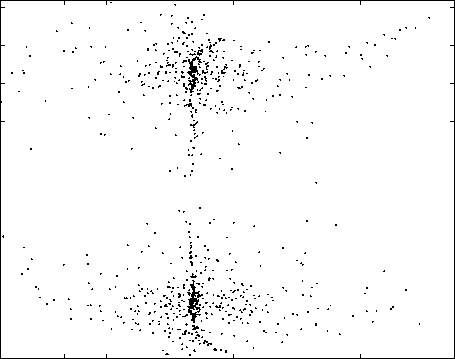
-0.03   -0.02   -0.01       0      0.01     0.02     0.03     0.04     0.05     0.06     0.07

Fig. 8. Separation performed by the RBF-based network.

0.04

0.02

0

-0.02

-0.04

-0.06

-0.08

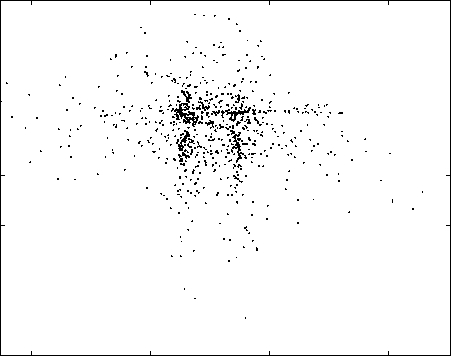
-0.03       -0.02       -0.01          0          0.01         0.02        0.03        0.04

Fig. 9. ICA result obtained with the RBF-based network without
regularization, in the case of the mixture of two supergaussians.

Table 1. Results obtained with the MLP- and RBF-based net-
works. The table shows the mean and standard deviation of the
number of training epochs needed to reach a specified mutual in-
formation at the outputs.

6. REFERENCES

[1] G. Burel, “Blind separation of sources: A nonlinear neural
algorithm,” Neural Networks, vol. 5, no. 6, pp. 937-947,
1992.

[2] G. Deco and W. Brauer, “Nonlinear higher-order statistical
decorrelation by volume-conserving neural architectures,”
Neural Networks, vol. 8, pp. 525-535, 1995.

[3] G. C. Marques and L. B. Almeida, “An objective function for
independence,” in Proc. International Conference on Neural
Networks, Washington DC, 1996, pp. 453-457.

[4] G. C. Marques and L. B. Almeida, “Separation of nonlin-
ear mixtures using pattern repulsion,” in Proc. First Int.
Worksh. Independent Component Analysis and Signal Sep-
aration, J. F. Cardoso, C. Jutten, and P. Loubaton, Eds., Aus-
sois, France, 1999, pp. 277-282.

[5] H. Valpola, “Nonlinear independent component analysis us-
ing ensemble learning: Theory,” in Proc. Second Int. Worksh.
Independent Component Analysis and Blind Signal Separa-
tion, Helsinki, Finland, 2000, pp. 251-256.

[6] L. B. Almeida, “Linear and nonlinear ICA based on mutual
information,” in Proc. Symp. 2000 on Adapt. Sys. for Sig.
Proc., Commun. and Control, Lake Louise, Alberta, Canada,
2000.

[7] L. B. Almeida, “Simultaneous MI-based estimation of inde-
pendent components and of their distributions,” in Proc. Sec-
ond Int. Worksh. Independent Component Analysis and Blind
Signal Separation, Helsinki, Finland, 2000, pp. 169-174.

[8] L. B. Almeida, “MISEP - linear and nonlinear ICA
based on mutual information,” Journal of Machine Learn-
ing Research, submitted for publication; available at
http://neuraLmesc-idpt/^lba/papers/jmlr03.pdf.

[9] A. Bell and T. Sejnowski, “An information-maximization ap-
proach to blind separation and blind deconvolution,” Neural
Computation, vol. 7, pp. 1129-1159, 1995.

[10] L. B. Almeida, “Multilayer perceptrons,” in Handbook of
Neural Computation, E. Fiesler and R. Beale, Eds. Insti-
tute of Physics, 1997, Oxford University Press, available
at http://www. iop.org/Books/CIL/HNC/pdf/NCC122.PDF.

[11] J. Moody and C. Darken, “Learning with localized recep-
tive fields,” in Proc. 1988 Connectionist Summer School,
D. Touretzky, G. Hinton, and T. Sejnowski, Eds. 1988, pp.
133-143, Morgan Kaufmann, San Mateo, CA.

<<   3   4   5   6  

More intriguing information