The name is absent

The solution of this differential equation is:

- -t/

(68)              V(t) = Vo e ^τ

or the voltage V drops e~2,72 times for time τ from the end of applied rectangular
impulse V0.

In space and time the dynamics of a single EPSP could be described by the
following generalized equation:

- x/ -1/

(69)             V( x,t) = Vo^{e λ}e ^τ

Here should be mentioned that the space constant λ depends on the diameter of
the dendrite, so we must decompose the dendritic tree into smaller segments
with approximately the same λ in order to be more precise in our calculations.
But if we need rough approximation we could consider that the dendrite has
constant diameter of 1μm and we can use the calculated value for the space
constant λ~353μm.

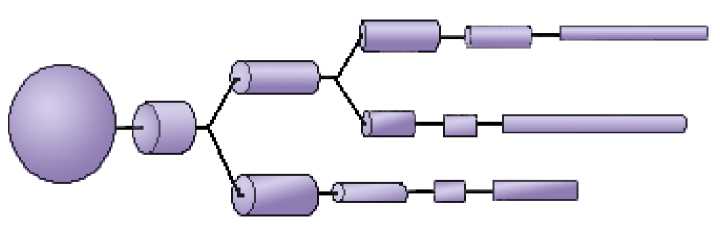
Fig. 9 Cable net approximation of the dendritic tree. Modified from Sajda (2002)

38

<<   35   36   37   38   39   40   41   >>

More intriguing information