h=i+l
h=i+k
h=i+j
h=i
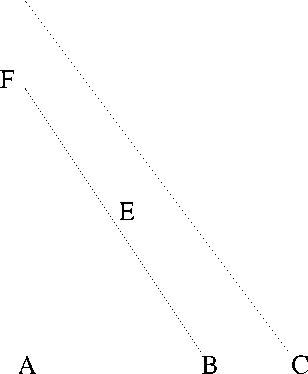
Figure 13: Example of c-commands.
5.2 Definition of C-command
Definition [13] p.134
Node A c-commands (constituent-commands) node B iff:
i) A does not dominate B and B does not dominate A,
ii) The first branching node dominating A also dominates B.
Remarks
The first requirement is that there is no direct route up or down from A to B
passing more than one higher node. The second requirement restricts A and
B to be ’close’. Haegeman’s first criterion for dominance needs to be adjusted:
if it is correct then h(A) > h(B) and h(B) > h(A) so that the set of all c-
commands is empty, therefore greater than or equal ≥ is used here instead of
greater than >. Haegeman’s second criterion for dominance also needs to be
adjusted: if no higher node is allowed the set of c-commands is again empty.
Chomsky (1986a) [6] p.161 approaches the sub ject in a different manner using
maximal projections.
Example:Figure 13 in the figure 0 < j < k < l. The corresponding ultra-
metric matrix is
• ABCD
A0kk l
(24)
U= B . 0 j l
C..0l
D. . .0
15
More intriguing information
1. The name is absent2. Computational Batik Motif Generation Innovation of Traditi onal Heritage by Fracta l Computation
3. Demand Potential for Goat Meat in Southern States: Empirical Evidence from a Multi-State Goat Meat Consumer Survey
4. Types of Tax Concessions for Promoting Investment in Free Economic and Trade Areas
5. How do investors' expectations drive asset prices?
6. FASTER TRAINING IN NONLINEAR ICA USING MISEP
7. A Computational Model of Children's Semantic Memory
8. The Demand for Specialty-Crop Insurance: Adverse Selection and Moral Hazard
9. AGRICULTURAL TRADE LIBERALIZATION UNDER NAFTA: REPORTING ON THE REPORT CARD
10. IMMIGRATION POLICY AND THE AGRICULTURAL LABOR MARKET: THE EFFECT ON JOB DURATION