Learning and Nonlinear Models - Revista da Sociedade Brasileira de Redes Neurais, Vol. 1, No. 2, pp. 122-130, 2003
© Sociedade Brasileira de Redes Neurais
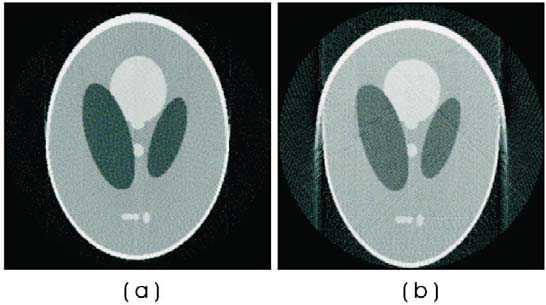
Figure 1: Reconstructed images from projections of the same synthetic phantom (Shepp-Logan) using parallel beam
reconstruction geometry. (a) Projections generated by parallel beam. (b) Projections generated by fan-beam (more realistic)
geometry lead to distorted image when parallel beam reconstruction is used.
Measuring the logarithm of the intensity ratio at different positions (s) for several angles (θ) leads to
p(s,θ) = ln
=∫ f(x, y)du
L
(2)
The pair (s,θ) represents the ray coordinates related to the object. s is the shift from the center and θ the angle at which
the measurement is obtained. The values p(s,θ) form a image that is the projection obtained from these external measurements.
This image is also called sinogram because a single point in the object (f(x,y)) is mapped to a sinusoid in this projection space.
The reconstruction problem is to obtain f(x,y) from the projection p(s,θ).
The Radon transform describes the direct problem or projection generation process. The inverse problem, or reconstruction
process can be calculated by the inverse Radon transform, but this is seldom used due to its complexity:
f (r,φ)
."ι∫π ∫+∞dp(sθds ■■
(3)
2π2 )Jo -∞ r cos(θ - φ)
where (r,φ) are polar coordinates of the image to be reconstructed. It can be shown that f(r,φ) can also be calculated by
backprojecting q(s,θ) a high-pass filtered version of p(s,θ) [10,11]:
π
(4)
f(r, φ) = ∫ q (r cos(θ - φ),θ)dθ
0
where the backprojection operation is simply the accumulation of the ray-sums of all the rays that pass through the point (r,φ).
Most equipments use filter backprojection as the reconstruction algorithm, because it is easier to calculate. Among other
methods less used are Fourier Reconstruction and ART (Algebraic Reconstruction Techniques).
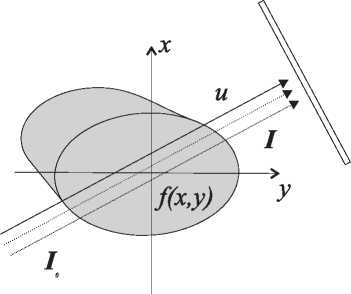
Figure 2: Radiation beam crossing an object, producing a “shadow” over the plate at the right-upper of figure.
123
More intriguing information
1. Expectations, money, and the forecasting of inflation2. Human Rights Violations by the Executive: Complicity of the Judiciary in Cameroon?
3. Types of Cost in Inductive Concept Learning
4. The name is absent
5. Valuing Farm Financial Information
6. The Shepherd Sinfonia
7. Improving behaviour classification consistency: a technique from biological taxonomy
8. The resources and strategies that 10-11 year old boys use to construct masculinities in the school setting
9. The name is absent
10. From music student to professional: the process of transition