TOMOGRAPHIC IMAGE RECONSTRUCTION OF FAN-BEAM PROJECTIONS WITH EQUIDISTANT DETECTORS USING PARTIALLY CONNECTED NEURAL NETWORKS

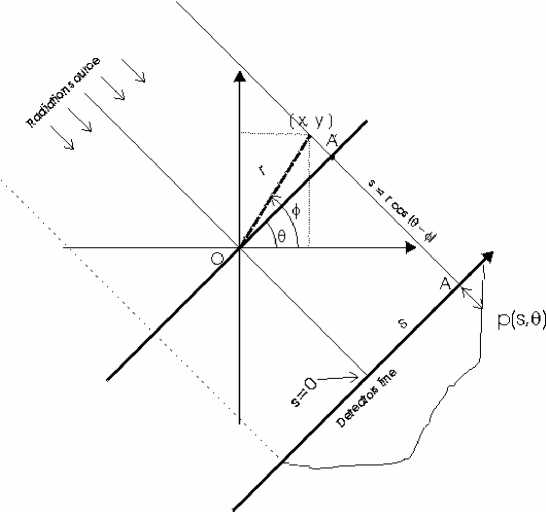
Figure 3: Geometric representation of projections with parallel beans.

Figure 3 illustrates the geometry of the problem for the parallel beam crossing the object yielding a profile over the
detectors line-arrange. Ideally, the detector at point A measures the amount of radiation due to only one ray yielding a
projection quantity p(s,θ), also called ray-sum for that point. The angle between OA’ segment and the x-axis is θ (or
equivalently the angle between ray direction and y-axis). The shift s corresponds to the OA’ segment modulus, and can be
expressed in terms of a generic point (r,φ) by the follow geometric relationship:

s = r cos(θ- φ)

(5)

This relation has fundamental importance in the tomographic reconstruction process, showing that the relationship
between projection and final image is purely geometric. It does not have any relation to the specific content of projections or
the final image.

So far, the explanation of tomographic reconstruction was based on parallel ray beam crossing the object. Many
equipments collect data in a fan-beam arrangement rather than parallel beam, allowing a single source of x-ray close to the
object and rapid collection of projections. When dealing with fan-beam projections, the source ray is considered punctual.
There are two kinds of fan-beam projections: equidistant and equiangular intervals between each detector along the line. In
this article we focused on equidistant intervals configuration.

Figure 4 shows a source located at point S, from a certain distance D to the origin emitting divergent rays at angle β.
The ray-sum at an angle β yields a projection value in the line detectors over the D1D2 segment. By transposing this line to an
imaginary segment D’1D’2 the shift s related to the OA’ segment can be computed by the expression [12],

ʌ, = r cos(^{β - φ})
U

(6)

where U is a weighting factor expressed in terms of the source to origin distance D:

U = ₁₊^{r sin}(^{β - φ})
D

(7)

When D approaches infinity, U tends to unity and expression (6) will match expression (5). Therefore, when the
source is positioned at a large distance from the object, fan-beam geometry will be equivalent to parallel ray beam geometry.

124