Learning and Nonlinear Models - Revista da Sociedade Brasileira de Redes Neurais, Vol. 1, No. 2, pp. 122-130, 2003
© Sociedade Brasileira de Redes Neurais

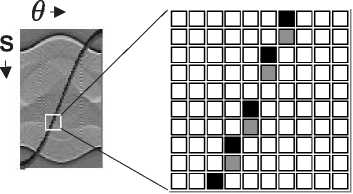
Figure 7: Zoom of part of the sinusoid, now showing the points located at gaps (in gray) used in the interpolation method.

It is clear from the equations (16) and (17) that the weights are complementary themselves,

u_i=1 -v_i

and both belong to the range [0,1].

The resulting single layer partially connected neural network to compute backprojection with fan-beam geometry and
interpolation is:

1^K

^f (^{r, φ}) = y_j =-∑[ ^ujkq (L⁵ J ^,θk )^+vj∣_cq (Γ⁵1 ^,θ )]                                                                         (17)

K k=1

where the synaptic weights are given by:

v_ji = U-²(Γ 5 J- 5 )                                                                                                                  (18)

and

v_ii = U^-2( 5 -L 5 J)                                                                                                                  (19)

It is worth mentioning that the backprojection algorithm using partially connected neural networks needs to run in two
distinct phases: the building phase where the relevant weights are calculated and the feeding phase where the filtered projection
is presented at the input and the values propagate to the output according to the weights giving the reconstructed image. The
building phase involves the weights calculated by equations (14) and (15) for parallel beam, or equations (18) and (19) for fan-
beam with interpolation geometry. The network structure is very similar, the main difference resides on the weights values.
Network for parallel beam reconstruction with no interpolation have only unity weights while network with interpolation or
fan-beam geometry have non-integer weight values.

2.2 Filtering Network

The high-pass filtering process required for the inverse Radon transform amplifies high spatial frequencies. To avoid excessive
noise amplification at these frequencies a band-limited filter, called Ram-Lak filter is often used [10,11,14]. The filter impulse
response is:

Only the first N values of n are considered, and the resulting FIR (finite impulse response) filter can be calculated by
convolving the filter impulse response with the input data, in this case the projection image p(5,θ). This convolution operation
is implemented as a single layer neural network with linear activation function according to previous works [5,6].

q(n,θ) = ∑^N h(n - k) p(5k,θ),      n=1,..,N

k=1

127

<<   <   3   4   5   6   7   8   9   >   >>