Learning and Nonlinear Models - Revista da Sociedade Brasileira de Redes Neurais, Vol. 1, No. 2, pp. 122-130, 2003
© Sociedade Brasileira de Redes Neurais

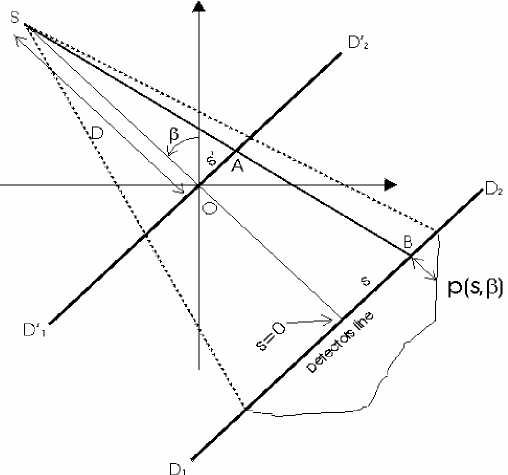
Figure 4: Geometric representation of projections given by fan-beam geometry.

In our approach, the filter backprojection is implemented by two partially connected neural networks with aim to
make good use of parallelism supplied by this structure to provide more speed in the reconstruction process [5,6]:
1. Partially connected neural network for filtering

2. Partially connected neural network for backprojection.

Next, we describe the backprojection neural network and modifications needed for the CT reconstruction with fan-beam
geometry.

2.1 Backprojection Network

The backprojection operation shown in equation (4) can be expressed for K discrete angle steps as:

1^K

f(r. r, φ) =   ∑ q ( r cos(θ - φ),θk )

K k=1

where the θ_k are the angles obtained at constant intervals Δθ. Each pixel in f(x, y)or in polar coordinate f(r, φ) will be the
summation of all ray-sums that had traversed that pixel. This represents the accumulation of the values along a sinusoid on the
(s,θ) plane as shown in figure 5.

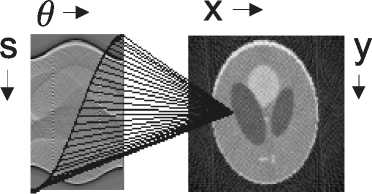
Figure 5: Backprojection process: contribution of (s, θ) pixels to a (x,y) pixel in the final image.

It was shown in previous works [5,6], that this equation can be implemented by a one layer feedforward network with
its weights previously determined in terms of the geometry of the problem. The expression of a fully connected neural network
with linear activation function is given by [13]:

N
y_j= ∑w_jix_i
i=1

125

<<   1   2   3   4   5   6   7   >>

More intriguing information