is independent of both the segments indices and the starting position. Hence,
Φ(bj-r-bj) = Φ(bj∙) =
exp[-∕3⅛(∣bj∙∣)]
/dbjexp[-∕J∕ι(∣bj∙∣)]
о ∖3∕2
—J exp [-3∣bj∣7(262)] .
(8.6)
The eqn. 8.5 is solved using Fourier transform and the boundary condition, p0(r, 0) =
J(r), to obtain
p0(R, N) = [3∕(27γ≡2)]3/2 exp [-3∣R∣2∕(2≡2)] , (8.7)
where R is the end-to-end vector of the chain, R = rjv - r0.
In SCFT, an elegant and particularly convenient continuous Gaussian chain model
is employed. This model is the continuum limit of the discrete Gaussian chain model
in which the polymer chain is viewed as a continuous, linearly elastic filament. The
configuration of the chain is specified by a space curve r(s) where s ∈ [0, N], as shown
in fig. 8. lb. The continuous variable s describes the locations of a segment along the
backbone of the chain. The potential energy of the continuous Gaussian chain can
be written as
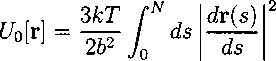
(8.8)
while the partition function is given by
Z0 = ʃ Drexp(-∕5t70[r]),
(8.9)
211
More intriguing information
1. The name is absent2. Ahorro y crecimiento: alguna evidencia para la economía argentina, 1970-2004
3. The name is absent
4. Fiscal Policy Rules in Practice
5. Confusion and Reinforcement Learning in Experimental Public Goods Games
6. The name is absent
7. Globalization, Redistribution, and the Composition of Public Education Expenditures
8. TINKERING WITH VALUATION ESTIMATES: IS THERE A FUTURE FOR WILLINGNESS TO ACCEPT MEASURES?
9. Pursuit of Competitive Advantages for Entrepreneurship: Development of Enterprise as a Learning Organization. International and Russian Experience
10. Demographic Features, Beliefs And Socio-Psychological Impact Of Acne Vulgaris Among Its Sufferers In Two Towns In Nigeria