where ʃ Dr denotes a functional integration. The potential energy is now a functional
of the space curve r(s) and partition function is calculated as a functional integral
over all the possible space curves. One approach to defining the functional integration
is to discretize the continuous function r (s) by a set of Ns + 1 equally spaces contour
points (r0, rɪ, ..., γλγJ. Hence,
Z0
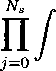
dvj exp

(8.10)
where b2∆s is the mean-squared length of one of the Ns bonds, and ∆s = N∕Ns is the
spacing between the contour points. The quality of the approximation improves as Ns
→ ∞. Again, the Chapman-Kolmogorov equation is used to obtain the probability
density distribution of the segments.
p0(r, s + ∆s) = Z d(Δr)Φ(Δr)p0(r — ∆r, s), (8.11)
where
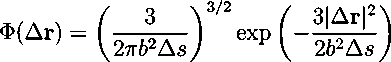
(8.12)
The Chapman-Kolmogorov integral equation 8.11 can be reduced to partial differen-
tial equations, which are referred to as Fokker-Planck equations by Taylor-expanding
both sides of the equation in powers of ∆s and ∆r and taking ∆s → O.
∂ . b2 2 / ʌ
—p0(r,s) = —V Po(r,s).
(8.13)
OS O
212
More intriguing information
1. Yield curve analysis2. Institutions, Social Norms, and Bargaining Power: An Analysis of Individual Leisure Time in Couple Households
3. Work Rich, Time Poor? Time-Use of Women and Men in Ireland
4. Nietzsche, immortality, singularity and eternal recurrence1
5. Crime as a Social Cost of Poverty and Inequality: A Review Focusing on Developing Countries
6. EU Preferential Partners in Search of New Policy Strategies for Agriculture: The Case of Citrus Sector in Trinidad and Tobago
7. The storage and use of newborn babies’ blood spot cards: a public consultation
8. The name is absent
9. The name is absent
10. O funcionalismo de Sellars: uma pesquisa histδrica