by
J^<7(r,s; [w]) = ^∙V2g(r,s; [w]) - w(γ)q(γ,s; [w]), (8.22)
with the initial condition, <γ(r, 0; [w]) = 1. The average segment density of the single
chain in presence of the external field is given by
p(r; [w]) = <ρ(r)>jw] =
ʃ Drp(r) exp (—Z3t70[r] - βUι[r, w])
ʃ Drexp (-βU0[r] - ∕3Dι[r,w])
1
VQ[w]
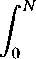
ds q(γ, N — s; [w])q(γ, s; [w]).
(8.23)
We can also derive the density of the segment located at the contour position, s,
^ɪɪ^(r, N-s- [w])9(r, s- [w]).
(8.24)
These results (eqs. 8.20 and 8.23) are for linear homopolymers. The derivation can
be generalized to a variety of chain structures, as shown in detail in ref. [269].
8.2 From particles to fields
The preliminary step in a field-based approach, such as SCFT, is to convert the
standard particle-based model to a statistical field theory. This particle-to-field trans-
formation technique for a homopolymer in an explicit solvent is discussed here in
detail. The intramolecular long-range interferences and inter-molecular interactions
between the segments of the polymer chains as well as the interactions with the sol-
215
More intriguing information
1. The Context of Sense and Sensibility2. Higher education funding reforms in England: the distributional effects and the shifting balance of costs
3. A methodological approach in order to support decision-makers when defining Mobility and Transportation Politics
4. On the estimation of hospital cost: the approach
5. Visual Artists Between Cultural Demand and Economic Subsistence. Empirical Findings From Berlin.
6. BUSINESS SUCCESS: WHAT FACTORS REALLY MATTER?
7. Proceedings of the Fourth International Workshop on Epigenetic Robotics
8. The purpose of this paper is to report on the 2008 inaugural Equal Opportunities Conference held at the University of East Anglia, Norwich
9. Implementation of Rule Based Algorithm for Sandhi-Vicheda Of Compound Hindi Words
10. Olive Tree Farming in Jaen: Situation With the New Cap and Comparison With the Province Income Per Capita.