The name is absent

Thus, the distribution probability density for a continuous Gaussian chain takes
the form of a conventional diffusion equation with a diffusion coefficient given by
b²∕6. This equation is solved to obtain the probability density, instead of the integral
Chapman-Kolmogorov equations with the initial condition, po(r,O) = J(r). The final
distribution is given by

z ʌ / ³ V^/2 f ³∣r∣²∖

= ^expΓ^J∙

In SCFT, the interaction potential of the surrounding polymer segments self con-
sistently generate the potential field on the the single polymer chain. Hence, the
theoretical formulation of a Gaussian chain in an external field is presented here. The
microscopic density of a Gaussian chain is given by

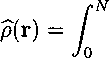
dsδ(r — r(s)).

(8.15)

Thus, the potential due to the external field (w(r) acting on the chain is given by

∕3t7χ[r, w] = / dr'w(r')p(r).

The partition function of the chain is

Z[w∖ — Drexp(-βU₀[r] — βUι[r,w[).              (8.17)

213

<<   222   223   224   225   226   227   228   >>

More intriguing information