To compute the extrinsic LLR for uk, we perform the follow-
ing computation:
Le(k) = maxS*k∈K(Λ(Sk∣u6 = 0) - Λ(sk∣u = 1))
-La(yks)-Lc(yks),(6)
where K is the set of all possible states and max * () is defined
as max * ( S ) = ln (∑ s∈S es ).
In the next section, we will describe how this algorithm is
mapped onto GPU in detail.
IV. Implementation of MAP decoder on GPU
A straight-forward implementation of the decoding algorithm
requires the completion of N stages of αk computation before
the start of βk computation. Throughput of such a decoder would
be low on a GPU. First, the parallelism of this decoder would be
low; since we would spawn only one thread block with 8 threads
to traverse the trellis in parallel. Second, the memory required
to save N stages of αk is significantly larger than the shared
memory size. Finally, a traversal from stage 0 to stage N - 1
takes many cycles to complete and leads to very long decoding
delay.
Figure 3 provides an overview of our implementation. At the
beginning of the decoding process, the inputs of the decoder,
LLRs from the channel, are copied from the host memory to
device memory. Instead of spawning only one thread-block per
codeword to perform decoding, a codeword is split into P sub-
blocks and uses P independent thread blocks in parallel. We
still assign 8 threads per each thread block as there are only
8 trellis states. However, both the amount of shared memory
required and the decoding latency are reduced as a thread-
block only needs to traverse through N stages. After each half
decoding iteration, thread blocks are synchronized by writing
extrinsic LLRs to device memory and terminating the kernel.
In the device memory, we allocate memory for both extrinsic
LLRs from the first half iteration and extrinsic LLRs from the
second half iteration. During the first half iteration, the P thread
blocks read from extrinsic LLRs from the second half iteration.
During the second half of the iteration, the direction is reversed.
Although a sliding window with training sequence [16] can be
used to improve the BER performance of the decoder, it is not
supported by the current design. As the length of sub-blocks is
very small with large P , a sliding window would add significant
overhead. However, the next iteration initialization technique is
used to improve BER performance. The α and β values between
neighboring thread-blocks are exchanged between iterations.
Only one MAP kernel is needed as each half iteration of the
MAP decoding algorithm performs the same sequence of compu-
tations. However, since the input changes and the output changes
between each half iteration, the kernel needs to be reconfigurable.
Specifically, the first half iteration reads a priori LLRs and writes
extrinsic LLRs without any interleaving or deinterleaving. The
second half iteration reads a priori LLRs interleaved and writes
extrinsic LLRs deinterleaved. The kernel handles reconfiguration
easily with a couple of simple conditional reads and writes
at the beginning and the end of the kernel. Therefore, this
kernel executes twice per iteration. The implementation details
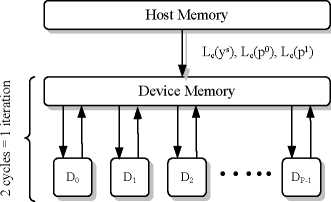
Fig. 3: Overview of our MAP decoder implementation
of the reconfigurable MAP kernel are described in the following
subsections.
A. Shared Memory Allocation
To increase locality of the data, our implementation attempts to
prefetch data from device memory into shared memory and keep
intermediate results on die. Since the backward traversal depends
on the results from the forward traversal, we save N stages of αk
values in shared memory from the forward traversal. Since there
are 8 threads, one per trellis state, each thread block requires
8N floats for α. Similarly, we need to save βk to compute βk-1,
which requires 8 floats. In order to increase thread utilization
during extrinsic LLR computation, we save up to 8 stages of
Λk (Sk ∣ub =0)and Λk (Sk ∣ub =1), which requires 128 floats.
In addition, at the start of the kernel, we prefetch N LLRs
from the channel and N a priori LLRs into shared memory
for more efficient access. A total of 10N +196 floats is allocated
per thread-block. Since we only have 16KB of shared memory
which is divided among concurrent executing thread blocks,
small P increases the amount of shared memory required per
thread block which reduces the number of concurrent executing
thread blocks significantly.
B. Forward Traversal
During the forward traversal, each thread block first traverses
through the trellis to compute α. We assign one thread to
each trellis level; each thread evaluates two incoming paths and
updates αk (Sj) for the current trellis stage using αk-1, the
forward metrics from the previous trellis stage k-1. The decoder
use Equation (2) to compute αk . The computation, however,
depends on the path taken (Sk-1, Sk). The two incoming paths
are known a priori since the connections are defined by the trellis
structure as shown in Figure 2. Table I summarizes operands
needed for α computation. The indices of the αk are stored in
constant memory. Each thread loads the indices and the values
pk ∣ub =0and pk ∣ub =1at the start of the kernel. The
pseudo-code for one iteration of αk computation is shown in
Algorithm 1. The memory access pattern is very regular for the
forward traversal. Threads access values of αk-1 in different
memory banks. Since all threads access the same a priori LLR
and parity LLR in each iteration, memory accesses are broadcast
reads. Therefore, there are no shared memory conflicts in either
case, that is memory reads and writes are handled efficiently by
shared memory.
194
More intriguing information
1. Visual Perception of Humanoid Movement2. Ultrametric Distance in Syntax
3. Les freins culturels à l'adoption des IFRS en Europe : une analyse du cas français
4. Innovation Policy and the Economy, Volume 11
5. Credit Markets and the Propagation of Monetary Policy Shocks
6. The Triangular Relationship between the Commission, NRAs and National Courts Revisited
7. The name is absent
8. The magnitude and Cyclical Behavior of Financial Market Frictions
9. SOME ISSUES IN LAND TENURE, OWNERSHIP AND CONTROL IN DISPERSED VS. CONCENTRATED AGRICULTURE
10. THE MEXICAN HOG INDUSTRY: MOVING BEYOND 2003