On the Desirability of Taxing Charitable Contributions

Appendix C: Derivation of Equation 16

We first re-formulate equation (15) in the main text for convenience.

(C1)

∂L∖

***

∂s I s=o,t ,T ,g ,z

∂ l^s ( w )
∂s

^dF ( w )

+ μ₁ - z - [1 - F(W)] - μ₃ - λ^s (W) - z

Differentiation of the Lagrangean in (14) with respect to z yields the following first-

order condition:

(C2)

∂L

****

∂z s =0,t ,T ,g ,z

ʃ[^ ' [V^s ( w )] - λ^s ( w )]dF ( w ) - μ₁ -1 -

∂l^s(w)

W--

∂z

^dF⁽^w )

+ (μ - μ2) - [1 - F(W)] - μ3 - λ^s( W) = 0.

Substituting for the term μ₃ - λ^s(W) from (C2) into (C1) yields:

∂L∣

***

∂s I s=0,t ,t ,g ,z

=μ₁ - z - [1 - F(W)] - z -

'[V^s(W)] -λ^s(W)]dF(W)

(C3)

fΓ ∂l^s ( W )

I w--—

J|_ ∂s

dF ( W ) + μ₁ -1 - z

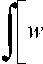
∂l^s(W )’

∂z

^dF⁽^w )

+ z - ∫[∏ ' '[V^s (w)] - λ^s (w)]dF(w) - (μ₁ - μ₂ ) - z - [1 - F(τ^)].

Re-formulating the budget constraint faced by an individual who engages in signaling
yields:

(C4) J (l, c, t, T, s, z) ≡ (1 -1) - w - (1 -1) + T - c - (1 + s) - z = 0 .

Differentiation of the expression in (C4) yields:

,_r.. ∂J, ∂J,

^(C5)^z^-- s =0^-- s=0 = 0.
∂z ∂s

Thus, for any ability level W, the following holds: