Substitution into (A5) yields:
(A9)
∂L
∂s s=0
- (μi - μ2) ∙ δ (1 - t) ∙
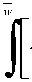
dF(w) + (μ -μ2)∙δ∙T∙
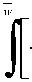
w
dF ( w )
+ (μi - μ2) ∙
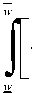
dF ( w ).
Consider next, the following optimization problem, where an individual, given some
choice of the level of charitable contributions, z, is choosing the level of the
consumption good, c, and leisure, l. Formulating the Lagrangean yields:
(A10) L(w, z, t,τ, s) ≡ max[h(l) + u(c) +ν∙[(1 -t) ∙ w∙(1-l) +T -c-(1 +s) ∙z]],
where ν denotes the Lagrange multiplier. Re-examining the effect of the small
perturbation in the tax system around the optimum, by fully differentiating the
Lagrangean in (A10), using the envelope theorem, yields:
(A11) di∣,=0, t,r =∆∙v[-.■ + δ-[(1 -1 ) ∙ w ∙ (1 -1 ) + T ]].
Denote by z*(w) , the optimal choice of the level of charitable contributions of the
individual with ability w, given the optimal tax system. By construction of the optimal
choice of the individual given the optimal tax system prior to the perturbation, it
follows that:
(A12)
∂v[z*(w)]
∂z
∂L[w,z*(w)]
∂z
=0.
s=0,t,T
After the perturbation, it follows, by virtue of (A11), that for any z < z*(w),
dL∖s=0, t,T
> 0 ; whereas, for any z > z*( w ), dL∖s=0, t, T
< 0. Thus,
(A13)
∂L[w, z*(w)]
∂L[w, z* (w)]
∂z
s=ds,t+dt,T+dT
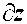
s=0,t,T
This implies that:
24