On the Desirability of Taxing Charitable Contributions

(A5)

^∑^-L=0 =^μι ∙ ^δ (^{1 - t}) ∙^t ∙
∂s

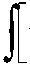
- μ₁ ∙ δ∙ T ∙ t ∙

dF ( w ) + ( μ - μ) ∙ δ∙T ∙

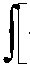
μι ∙^t ∙

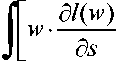
^dF(w) + (μ ^-μ₁)∙

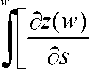
dF ( w ).

^dF (w ) ^- ( μ ^- μ₁) ∙ ^δ∙(l^-1 ) ∙

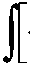
w

We need to prove that the sign of the derivative in (A5) is negative. We first turn to
further simplify the expression on the right-hand side of (A5). Consider the following
optimization problem, where an individual, given some labor/leisure choice, l, is
choosing how to allocate the net income across consumption good, c, and charitable
contribution, z. Formulating the Lagrangean yields:

(A6)   L(w, l, t,τ, s) ≡ max[u(c) +v(z)+ν∙ [(1- t)∙w ∙ (1 -l)+ T- c- (1 +s)∙ z]],

where ν denotes the Lagrange multiplier. Now consider a small change in the tax
system around the optimal linear labor income tax system (set for s=0), which is
defined as follows: ds = ∆,dt = -∆ ∙δ∙ (1 -t) and dT = ∆∙ δ∙ T , where ∆ > 0 and is
arbitrarily small. Fully differentiating the Lagrangean in (A6), using the envelope
theorem, then yields:

(A7) dL∖,=o,,T =∆∙v[-z+ δ∙[(1 -1 ) ∙ w ∙ (1 -1 ) + T ]] = 0,

where the last equality holds for any 1, by virtue of the homotheticity [see (A4)] and
the separability assumptions. It follows that the optimal labor/leisure choice of an
individual of ability w (for all w) is unaffected by the suggested small perturbation in
the tax system around the optimum. Thus, for all w, it follows that:

(A8) - δ∙(1 -1 )∙^dw +^dw + δ∙T.≡¹*w* = 0.

∂t    ∂s        ∂T

23

<<   21   22   23   24   25   26   27   >>

More intriguing information