Appendix A: Proof of Proposition 1
We assume that second order conditions are satisfied, thus it suffices to show that
there exists a marginal welfare gain by slightly decreasing the tax rate on charitable
contributions from s=0. Differentiating the Lagrangean in (12) with respect to t, T
and g yields the following first-order conditions (suppressing the tax parameters to
abbreviate notation):
(A1)
(A2)
W '[V ( w )] ∙ λ( w ) ∙ w
ww
+μ ∙ [w∙[1 -l(w)]]dF(w)+(μ-μ2)∙
ww
⅛ =0 = [WT(w)]∙λ(W)]dF(W)-μ ∙t∙ f[w∙dlw
∂Tj JL ∂T
WW
+ (μ1 — μ2) ∙
w
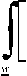
dF ( w ) - μ = 0,
• [1 -1 ( w )]] dF ( w ) - μ1 ∙ t ∙
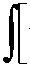
dF ( w )
dF ( w ) = 0,
dF( w )
w
∂L
(A3) — , =0 =α∙r∙(g)∙ l[W,[V(W)]]dF(w)-(μ -⅛) = 0.
∂g
w
By virtue of the homotheticity assumption, one can write the optimal choice of an
individual of ability w as follows:
(A4) z(w) = δ ∙[(1 -1) ∙ w ∙ [1 -1(w )] + T] /(1 + ,),
where 0 < δ< 1 and δ is independent of w.
Substituting for z(w) from (A3) into (13), following some algebraic manipulations
employing (A1) and (A2), and re-arranging, yields the following simplified form of
the derivative in (13):
22
More intriguing information
1. he Effect of Phosphorylation on the Electron Capture Dissociation of Peptide Ions2. The name is absent
3. The name is absent
4. 03-01 "Read My Lips: More New Tax Cuts - The Distributional Impacts of Repealing Dividend Taxation"
5. The name is absent
6. Geography, Health, and Demo-Economic Development
7. Voluntary Teaming and Effort
8. TOMOGRAPHIC IMAGE RECONSTRUCTION OF FAN-BEAM PROJECTIONS WITH EQUIDISTANT DETECTORS USING PARTIALLY CONNECTED NEURAL NETWORKS
9. Long-Term Capital Movements
10. A Dynamic Model of Conflict and Cooperation