The sign of |A1| and |A2| depends on the sign and magnitude of α and β and is thus ambiguous.
Using Eqs. (25) and (26) the slopes of the best-response functions (24) are:
∂si _ β ( tikii + ki ) + α
∂ti = ∣A∣ ’
∂sj βtj kji - α
∂tf = Й ’
∂τ b00(gi)b00(gj)tjktji + b00(gi)b00(gj)(tiktii + ki)
∂)ti = Й
A.2 Proof of Proposition 3
Proposition 3 is proved by establishing two lemmata. Lemma 1 states conditions for td to be
greater, equal, or lower than tN . Lemma 2 presents a refined condition pertaining to cases (i),
(ii), and (v) listed in table 1.
Lemma 1: If siti ≥ 0 the capital tax rate under decentralized leadership exceeds the capital
tax rate under both-sided Nash behavior, i.e. td > tN . If siti < 0, the effect on the tax rate ti is
given by
-li τti
I b0(gi)⅛ I ≠- td
<
>
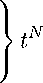
(27)
Proof: The optimal state behavior is characterized by Eq. (21). Thus, starting from the
Nash outcome tN , as characterized by Eq. (9), state i’s incentive to deviate from tN depends on
the terms Vgisiti and Vτiτti . By Eq. (5) Vτiτti = -liτti which following Eq. (18) is positive. Note,
Vgisiti = b0(gi)siti . If b0(gi)siti is non-negative (case (iii) and (iv)), state i can increase after-tax
labor income as well as local public good provision by setting td > tN . To prove the second
assertion, consider the opposite case. If siti < 0 and -liτti > (<) Ib0(gi)siti I, state i can improve
utility of the representative household by choosing td > (<) tN . For the special case siti < 0 and
-liτti = I b0(gi)siti I the opposite effects nullify each other and td = tN. □
27
More intriguing information
1. THE CHANGING STRUCTURE OF AGRICULTURE2. Structure and objectives of Austria's foreign direct investment in the four adjacent Central and Eastern European countries Hungary, the Czech Republic, Slovenia and Slovakia
3. Heavy Hero or Digital Dummy: multimodal player-avatar relations in FINAL FANTASY 7
4. Mortality study of 18 000 patients treated with omeprazole
5. Manufacturing Earnings and Cycles: New Evidence
6. Visual Artists Between Cultural Demand and Economic Subsistence. Empirical Findings From Berlin.
7. Segmentación en la era de la globalización: ¿Cómo encontrar un segmento nuevo de mercado?
8. Perfect Regular Equilibrium
9. Personal Experience: A Most Vicious and Limited Circle!? On the Role of Entrepreneurial Experience for Firm Survival
10. MULTIPLE COMPARISONS WITH THE BEST: BAYESIAN PRECISION MEASURES OF EFFICIENCY RANKINGS