Uncertain Productivity Growth
4 TIMING & COMPARATIVE STATICS
By using the Girsanov theorem12 it is possible to derive the probability density function of Ti* as
f (Ti*,⅜Λ*) =
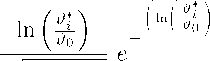
2
1 1 2 ʌ τ, * ʌ
-(α-1σ )Ti I
2σ2T *
i
√2πσ2T*3
(69)
which is also referred to as the Inverse Gaussian distribution.13 The Laplace transform of Ti* is
then given by (see Ross, 1996; Proposition 8.4.1)
e-λTi* = 0∞
λTi*
f(Ti*)dTi*
ι ln ( '
e- ( (α (α-2 σ2 )2+2σ2λ-(α-1 σ'2)'j σl
(70)
and can be used to determine the expected time before market entry as
∞ ∂E(e-λTi*)
E(T*)=/ T*f (T*)dT* = - lim (m )
0 λ→0 ∂λ
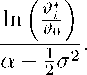
(71)
More precisely, the expected time before market entry results in both modes as (see Karatzas
and Shreve, 1991)
1
α- 2 σ2
ln
if α > 2 σ2
e(TV = о =
(72)
∞ if α ≤ 2 σ2
with ■&* >⅜ and i ∈{E,F}.
Equation (72) shows that for σ ∈ (0, √2α) there exists a finite market entry time. However, if
productivity growth α is lower than 2σ2 or equal to zero, market entry might not be realized
since E(Ti*) diverges.14
Within the proximity-concentration trade-off framework it is again possible to derive a relation-
ship between relative fixed and variable costs which determines whether the expected market
12 A detailed derivation is offered by Karatzas and Shreve (1991, p.196) or by Karlin and Taylor (1975, p.363).
13 The name ”inverse gaussian distribution” stems form the inverse relationship between the cumulant generating
functions of these distributions and those of Gaussian distributions.
14 A detailed discussion about the peculiarities of the inverse gaussian distribution can be found in Johnson, Kotz,
and Balakrishnan (1995) or Dixit (1993).
30
More intriguing information
1. Who runs the IFIs?2. The name is absent
3. Financial Markets and International Risk Sharing
4. Insurance within the firm
5. The name is absent
6. The Economics of Uncovered Interest Parity Condition for Emerging Markets: A Survey
7. The constitution and evolution of the stars
8. The name is absent
9. Imitation in location choice
10. Sustainability of economic development and governance patterns in water management - an overview on the reorganisation of public utilities in Campania, Italy, under EU Framework Directive in the field of water policy (2000/60/CE)