Uncertain Productivity Growth and the Choice between FDI and Export

Uncertain Productivity Growth

By integrating the probability density function (69) it is possible to derive the corresponding
cumulative distribution functions as

(74)

with ⅛ << and i ∈{E,F}.

* *■*

Expected Market Entry Time Te, Tf

(a) ¾ < ⅛F, α = 0.04,⅛0 = 1,σ = 0.1, but
FF (ð) > FE (ð) with κ = 1

(b) ¾ < ⅛F, α = 0.04,⅛₀ = 1,σ = 0.16, but

FF (tf) > FE (tf) with κ = 1

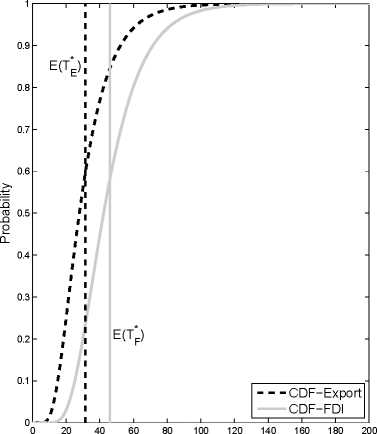
Figure 8: Cumulative Distribution Functions of Ti*.

Panel a) in figure 8 represents the cumulative distribution functions of both investment strategies
for a relative cost constellation which leads to a productivity cut-off ranking with tf*E < &р. The
vertical dashed line represents the export mode’s expected market entry time and the s-shaped
curve its cumulative distribution function. The continuous curves represent the FDI mode. In
the underlying example the export mode exhibits a first-order stochastic dominance over the FDI
strategy. Differently expressed, for any market entry time T_i^* , the probability of market entry
through exports will always be higher than in the FDI case. However, for the chosen relative cost
pattern, the FDI mode exhibits a higher option value (see figure 7, areas F2 , F3) and therefore

32

<<   31   32   33   34   35   36   37   >>

More intriguing information