Uncertain Productivity Growth and the Choice between FDI and Export

Uncertain Productivity Growth
the investor will neglect the export market entry for the sake of the FDI mode. The distance
between E(TFF) and E(TE) in figure 8 represents the prolongation of market entry by negligence.
Inversely, it can be concluded that for relative cost patterns which lead to a productivity cut-off
ranking with i?F. < ¾, the FDI mode has a first-order stochastic dominance over the export
mode and there will be no market entry prolongation.

By considering the partial derivative of equation (71) with respect to σ it is possible to assess the
impact of a volatility change in productivity on the expected market entry time. The differential
results as

∂E(T*)          1        ∕tf*λ         1      1 ∂tf*

-- ⁱ = _σ-------_l ln — +-------

^dσ       (α - 1 )2   Vo∕   (α - 1 σ²) tf* ^dσ

, C           ,        1 O

with ~^l > 1 and α > 2σ².

Thus, whether a change in uncertainty results in a positive or negative effect on the expected
market entry time, decisively depends on the partial differential on the right hand side of equation
(75). A change in uncertainty affects the optimal productivity levels tf* through two channels.
The first effect of an increase in σ is a rise in the option value of each market entry mode which
is captured by

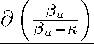
∂σ

The intuition for this monotonic positive effect is that an increase in uncertainty, incentivises the
postponement of the investment decision into the future (higher #*) in order to gain additional
information on the productivity development.

The second effect is a change in the expected investment value ½(tf) which itself depends on the
adjusted discount rate δ_u⁰ .

For linear periodical cash-flows (κ = 1) the discount rate becomes independent of σ with

∂δu = 0.                                       (77)

∂σ

Summing up theses two effects, in this particular case both market entry modes’ expected market
entry time strictly increases in σ . Furthermore, since the productivity cut-offs of both entry

33

<<   32   33   34   35   36   37   38   >>

More intriguing information