country i faces the following inverse demand schedule in country j:9
1
_1
Pij W = (j ^σ (Pj )σ-
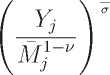
(3)
Profit maximizing firms allocate sales across markets such that marginal revenues are
equalized. This implies pij∙ [^] = τjpii [^] for all markets j on which a firm φ based in
country i is active. Operating revenues of firms based in country i from sales to market
j are therefore equal to Rij∙[^] = pij∙[φ]qij[φ]∕τij. Total revenue of an intermediate input
producer based in country i with productivity φ, is then given by:
1
N T τI-σY ∖ σ
Ri(^l = ∑ Iij ⅛ Ivlσ-1 (Pj)σ-1 (⅛j .
(4)
where Iij [v] is an indicator function that takes value one if a firm in country i with
productivity v is active on market j and zero otherwise.
2.2 The Labor Market
Firms operate with linear production functions qij [v] = vLij [v]. where Lij [v] is the level
of employment at firm v in country i for production of goods destined for country j .
Our model is in discrete time and all payments are made at the end of each period. At
the end of each period, firms and workers are hit by two different types of shocks: With
probability χ a job is destroyed due to a match-specific shock and with probability δ firms
are forced to leave the market. Assuming independence of these shocks, the actual rate
of job separation is given by η = δ + χ - δχ.
The flow costs of posting a single vacancy in country i are proportional to the pa-
rameter ci and measured in units of the final good. This implies that hiring costs are
linear in the number of workers to be recruited. As usual, the number of matches formed
in each period is given by a constant-returns-to-scale matching function. We denote by
mi[θi] = mi (θi)-ai the share of posted vacancies v filled each period, where θi is the
vacancy-unemployment ratio in country i and fai measures the efficiency of the labor
market in country i, while αi is the elasticity of the matching function. The rate at which
unemployed workers find employment is θimi [θi] . an increasing function of θi .
Each period, an intermediate input producer v in country i decides (i) about the
optimal number of vacancies to post vi [v], anticipating the wage which will be bargained
with the workers, and (ii) how to allocate total production over the domestic and the N-1
foreign markets. Problem (ii) features a decision on the extensive margin (which markets
to serve, i.e., on Iij [v]) and on the intensive margin (how much to sell on each market,
i.e., qij [v]). We relegate the market entry problem to section 2.3. Here it suffices to note
9Note that pij [.] is the cif price in market j and qij [.] is the quantity produced for that market,
including the iceberg transport costs.
More intriguing information
1. PROJECTED COSTS FOR SELECTED LOUISIANA VEGETABLE CROPS - 1997 SEASON2. INTERPERSONAL RELATIONS AND GROUP PROCESSES
3. The name is absent
4. Better policy analysis with better data. Constructing a Social Accounting Matrix from the European System of National Accounts.
5. A MARKOVIAN APPROXIMATED SOLUTION TO A PORTFOLIO MANAGEMENT PROBLEM
6. The name is absent
7. Deletion of a mycobacterial gene encoding a reductase leads to an altered cell wall containing β-oxo-mycolic acid analogues, and the accumulation of long-chain ketones related to mycolic acids
8. Sector Switching: An Unexplored Dimension of Firm Dynamics in Developing Countries
9. The name is absent
10. The name is absent