VPC=
2
μ0
σ2 + σμ0
This indicates the percentage of the variance that can be attributed to differences between studies.
Meta-Significance Testing
Stanley (2008) and Stanley (2005) note that a logarithmic relationship exists between the t-statistic and
the degress of freedom. A positive relationship between the two provides a confirmation of the empirical
effect (Stanley, 2005, 2008). A variation of Equation (8) is to use the natural log of the reported degrees of
freedom in each study, that is
ln |tij | = δ0 + δ1 ln(dfij )
Other versions also employ either the square root of the degrees of freedom (√df ) or the natural log of
the sample size (lnN) in place of ln(df) (examples of empirical work in this area include, Doucouliagos
and Stanley, 2005, 2008, Rose and Stanley, 2005, Stanley, 2005, 2008, Stanley, et al., 2008). This is the
meta-significance testing (MST) approach and is explored in the present analysis to ensure the robustness of
our results. In the MST, δ1 6= 0 indicates the presence ofa genuine effect. Stanley (2005, 2008) note that an
effect exists when δ1 = 2. In the log-linearised model shown above rejecting δ1 ≤ 0 indicates the existence
of an empirical effect (Stanley, 2005, Stanley, et al., 2008). According to Stanley (2005) the estimates in the
MST regression can be affected by publication selection. However, publication bias is proportional to the
inverse of the square root of the sample size (n- 2 ) in the presence of publication selection (Stanley, 2005).
Publication selection reduces the positive coefficient on the log of degrees of freedom thereby resulting in
a coefficient that is less than half (Stanley, 2005).
Yet another way of testing for a genuine empirical effect is to shrink the coefficients to zero by correcting
for publication bias (Stanley, 2005). Then a regression of the corrected t-statistics on precision should yield
an answer to whether there are is any genuine empirical effect.
corrected
∣tij | = ∙,∙ + φι
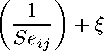
- tij = φ{s1j1)
+ε
In MST, the alternate hypothesis (H1) δ1 > 0 implies a genuine empirical effect. Similarly, φ > 0 and
φ 6= 0 indicates publication bias and a genuine empirical effect respectively. In the joint PET/MST β1 6= 0
(in Equation (8) - (9) and α1 = 0 in Equation (10)) and δ1 > 0 indicates a genuine empirical effect (Stan-
ley, 2005).
Finally, following Stanley (2005) and Stanley, et al. (2008) we carry out a t-test of β0 in Equation (8) and
(9) to test for publication bias (funnel asymetry test (FAT) anda test of β1 = 0 which provides the precision-
effect test (PET). This is similarly done for α0 and α1 to test for FAT and PET respectively. Stanley (2005)
also notes that a useful strategy is to carry out joint PET/MST testing to identify genuine effects in the
presence of publication bias. This is also carried out in the results section. Controls included in Equation
(9) and (10) allow us to check whether the reported estimates in the studies are strongly influenced by study
characteristics.
More intriguing information
1. Density Estimation and Combination under Model Ambiguity2. The name is absent
3. The name is absent
4. The storage and use of newborn babies’ blood spot cards: a public consultation
5. Effects of a Sport Education Intervention on Students’ Motivational Responses in Physical Education
6. Hemmnisse für die Vernetzungen von Wissenschaft und Wirtschaft abbauen
7. The name is absent
8. The open method of co-ordination: Some remarks regarding old-age security within an enlarged European Union
9. From music student to professional: the process of transition
10. Work Rich, Time Poor? Time-Use of Women and Men in Ireland