American trade policy towards Sub Saharan Africa –- a meta analysis of AGOA

of the variance. The confidence intervals for both models are then given by CI = θ + 1.96 × √Vθ . The
weights for the REM are differentiated by the superscript REM.

There is consensus in the literature that the REM is a preferred estimator when coefficient estimates are
heterogeneous. The FEM performs poorly in the presence of heterogeneity. However, in the absence of
heterogeneity the FEM can be used to obtain unbiased estimates of the summary study effect (Borenstein,
et al., 2009). Furthermore, Borenstein, et al. (2009) points out that the FEM can be performed on two or
more studies unlike the REM which requires a decent sample size. In the presence of heterogeneity, it is
useful to investigate the sources of the heterogeneity. In this paper, we pursue this by estimating our REM
model by study as well as using an MRA to investigate the sources of heterogeneity. We are able to carry
out tests of heterogeneity using the 1² statistic (1² = ( Q-^df ) × 100). This allows us to decide on the type
Q

of modelling to carry out. Borenstein, et al. (2009) citing Higgins et al (2003) suggest that values of 25%,
50% and 75% can be considered as low, medium and high heterogeneity respectively. An I² value of 0%
implies that there is no real variation in the studies while a value of 100% indicates high heterogeneity and
real variation among coefficients reported by the individual studies.

Meta-regression model

In carrying out the MRA, we need to emphasis that when there are several coefficients involved one needs
to be careful in the choice of MRA to apply. Questions of which coefficient to choose to represent each
study becomes difficult to answer. Secondly, the presence of more than one coefficient per study also poses
problems. Some authors get around this problem by selecting particular estimates or using the mean, mode
or other value of the study effects. In this paper, we choose to include all estimates and due to that we also
pursue a multi-level MRA to account for the multiple coefficients per study to check the accuracy of our
pooled MRAs. The MRA takes the following form

b

Se ≡ tij = ^β0 + ^β1

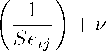
tij = β0 + β1

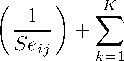
γk Zij k

-------+ ν

Seij ⁺

^K ζk Zjk

I⁺ X S^+μ0j⁺ eij
k=1   e^ij

var(eij) = σ2 ; var(μ_0j) = σ2o ; eij ~ iid(0,σ2); μoj ~ iid(0,σ20)

Where b_ij is the i^th coefficient from thej^th study, t_ij is the reported t-statistic of the i^th estimate in the j^th
study, Seij is the reported standard error, Zijk measures characteristics in each study—those that explain
the differences between studies as well as certain features of each particular study, ν is the disturbance term,
μ₀j is study level random intercept and e_ij is the error term. Estimation is carried out using weighted least
squares (WLS).

Equations (8) and (9) will be estimated by WLS while Equation (10) is a multi-level equation with studies
at level 2 and coefficient estimates at level 1. For Equation (10), α0 is assumed to be the same for each
study. The study level component (μ₀j ) represents the departure of the j^th study’s intercept from the overall
population intercept (α0). The first two coefficients are the fixed part of the model and the last two terms
provide us with the random variation (Goldstein, 1998). The variance partition component (VPC) can be
calculated as

<<   <   3   4   5   6   7   8   9   >   >>