In this same way, we decompose the other three elements of matrix and we rece-
ive:
4 5 5 _ 5
9 I__9 9 _|__9
(I - βP)-1
(1-β) + (1-0,1β) (1-β) + (1-0,1β)
4 _4 5 4
9 9 9 9
(1-β) + (1-0,1β) (1-β) + (1-0,1β)
Finally formula (15) becomes the following form:
(I - βP)-1
(1 - β)
0, 1β
We can check that the first matrix with factor 1/ (1 - β) is ergodic matrix of Mar-
kov Process for given stochastic matrix of transition P . The second matrix is so
named difference matrix. The sum of elements is equal zero in rows of this matrix.
Taking formula (19) into consideration, we receive total finite expected reward:
ν∞ (β) =
1
(1 - β)
' 4
9
4
. 9
9 +--------
9 1 - 0,1β
• q.
Now we can find value ν∞ (β) for two different β, β1 = 0, 5 and β2 = 0, 99.
After providing of values and simple calculations we receive:
ν∞ (0, 5) =
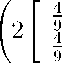
5
9
5
9
+ 1, 052
-3
Hence we obtain for the starting state and n → ∞
ν1,∞ (0, 5) = 2 • 1 + 1, 052 • 5 =
7, 260,
More intriguing information
1. The name is absent2. The name is absent
3. Les freins culturels à l'adoption des IFRS en Europe : une analyse du cas français
4. Testing Hypotheses in an I(2) Model with Applications to the Persistent Long Swings in the Dmk/$ Rate
5. The name is absent
6. The name is absent
7. AN EXPLORATION OF THE NEED FOR AND COST OF SELECTED TRADE FACILITATION MEASURES IN ASIA AND THE PACIFIC IN THE CONTEXT OF THE WTO NEGOTIATIONS
8. Regional dynamics in mountain areas and the need for integrated policies
9. Agricultural Policy as a Social Engineering Tool
10. BARRIERS TO EFFICIENCY AND THE PRIVATIZATION OF TOWNSHIP-VILLAGE ENTERPRISES