The paper is organized as follows. In the next section we introduce the KS distri-
bution family, while in third section we present the results of a Monte Carlo study on
the dependence structure of the distribution when the marginals are skewed Student t,
generalized secant hyperbolic and exponential power. Then, in section 4 we show the
results of an application to four market indices and conclusions are left to section 5.
2 KS formulation
Koehler and Symanowski (1995) introduce a class of multivariate distribution families
which can be built for almost any given univariate marginal distribution and can be
viewed as a generalization of the Cook-Johnson family of distributions (Johnson, 1987;
Cook and Johnson, 1981, 1986). Therefore, consider the р-dimensional random variable
U = (tʃi, U2,..., Up)' with support on the unit hypercube (O, I]'' and cdf
P P
F(u1,u2,...,up) = ɪɪ/, ɪɪ C~ja'3,
i=l j=i+l
(1)
where
Cij = u'°'+ + - uila'+u-la,+ , (2)
with ctij = Oiji > O for all (г, j) and α⅛+ = α∣ι + oii2 ÷ ∙ ∙ ∙ ÷ α⅛, > O for all i = 1, 2,..., p.
Deriving the cdf respect to uɪ, u2,..., up we obtain the probability density function
(pdf) of U which can be written as
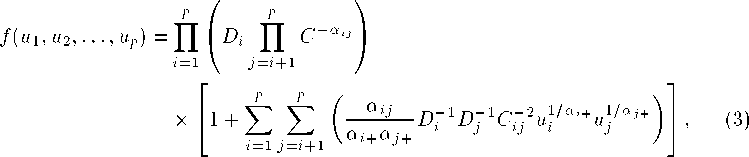
where
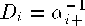
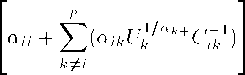
and Cij = Cji is defined by (2).
Koheler and Symanowski (1995) have shown that it is possible to obtain a scheme
to generate this distribution using gamma distributions. In this sense, let Yι, Y2,..., Yp
be i.i.d. Gamme(I1I) and, independently, Gu,Gi2, ...,Gpp be Gamma(oiij, 1) with
Gij. = ∑j=ι Gij. Then, the joint pdf of
Ui = (l + K√Gi+)^"'+, i= 1,2,...,p,
(4)
has cdf given by (1).
The conditional means of U are not linear functions of the values of the conditioning
variables. Consequently, it is more reasonable to measure dependence between variables
using concordance coefficients as the Kendall’s tau or the Spearman’s rank correlation
than using the correlation coefficient. However, the level of association between pairs
of variables in (3) depends on the level of the parameters (¾. In particular, the cdf
of any bivariate marginal (U, Uj) approximates the Frechét upper bound as ɑʊ —> O
and at the same time (cq+ — <¾)∕⅛-∣. —> O and (oy+ — oiij)∕oij+ —> O; vice versa, it
approximates (UUj), paired independence, if ɑʊ —> O when α⅛+ and αy+ are greater
than zero and at the same time α⅛+ —> ∞ and αy+ —> ∞. Moreover, the standard
form of U determines that all the correlations are positive. Variations in the standard
More intriguing information
1. Tastes, castes, and culture: The influence of society on preferences2. Who runs the IFIs?
3. LOCAL CONTROL AND IMPROVEMENT OF COMMUNITY SERVICE
4. THE RISE OF RURAL-TO-RURAL LABOR MARKETS IN CHINA
5. On the Relation between Robust and Bayesian Decision Making
6. The name is absent
7. The name is absent
8. LABOR POLICY AND THE OVER-ALL ECONOMY
9. Thresholds for Employment and Unemployment - a Spatial Analysis of German Regional Labour Markets 1992-2000
10. The Impact of Financial Openness on Economic Integration: Evidence from the Europe and the Cis