Skew Generalized Secant Hyperbolic. A random variable X has a skew generalized
secant hyperbolic distribution with parameters к > 0 and λ > — π is its density is
/ ɪ ʌ ___________Cl___________
∖ 1 + ɪ J a + cosh (c2 κ~ssn(x')χ) ,
where
a = cos(A),
« = 1,
a = cosh(λ)
|
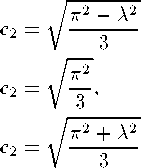
and |
Cl |
sin(λ) = ^Γc2 |
if λ ∈ |
( —7Γ, 0), |
|
and |
Cl |
= C2 |
if λ = |
0, |
|
and |
Cl |
sinh(λ) = ^^C2 |
if λ > |
0. |
The skew logistic distribution is a special case of this distribution when к ψ 1 and
ʌ = 0.
The cdf of X is given by
-P1SGSH («) =
(τ⅛∙) g(kx)
< 1 - fττ⅛) G(-)
у 1+я 2 J V к >
for X < 0,
for X > 0,
where
ɪ + ɪ tan 1 [tan (ʌ) tanh (^-æ)]
G(x) = < 1 [1 ÷ tanh (^-æ)]
ɪ + ɪ tanh 1 [tanh (ʌ) tanh (⅛Jr)]
for λ ∈ ( —7Γ, 0),
for λ = 0,
for λ > 0,
is the cdf of the symmetric generalized secant hyperbolic distribution with zero mean
and unit variance obtained when к = 1. Moreover, the moments of order r, r = 1, 2,...,
are:
E(Xr)
c1 Γ(r + 1)
2⅛+1√α2 - 1
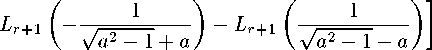
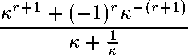
where Lr (∙) indicates the polylogarithmic function whose primary definition is1
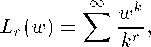
Iw∣ <1, w ∈ (D.
Skew Power Exponential. A random variable X has a skew exponential power
distribution (SEP) with parameters к > 0 and β > 0 is its density is
Jsep (^) = (ɪ) r = r °2 ɑə '' eχP [~cβκ 2-sr",∙''i∣.∕∙∣2-] ,
with c = Γ J Γ 1 ɪhe skew Laplace distribution is a special case of the SEP
when к ≠ 1 and β = ɪ. Likewise, when β = 1 we obtain a normal distribution.
1See at the web page http://functions.wolfram.com/10.08.02.0001.01
More intriguing information
1. A Study of Adult 'Non-Singers' In Newfoundland2. Regional differentiation in the Russian federation: A cluster-based typification
3. Migration and Technological Change in Rural Households: Complements or Substitutes?
4. Wounds and reinscriptions: schools, sexualities and performative subjects
5. Endogenous Determination of FDI Growth and Economic Growth:The OECD Case
6. The name is absent
7. The name is absent
8. Word searches: on the use of verbal and non-verbal resources during classroom talk
9. The name is absent
10. Heterogeneity of Investors and Asset Pricing in a Risk-Value World